Binary indexed trees, also called Fenwick trees, store partial sums in an array so prefix sums and point updates both run in logarithmic time. This structure keeps a compact view of the cumulative values in a base array and relies on binary index rules to decide which entries need to change on an update and which entries contribute to a prefix sum query.
Fenwick Tree Array Layout
A Fenwick tree keeps its data in a one dimensional tree[] array that sits beside a logical base array, often called arr[]. The base array holds the original values, and the tree array holds partial sums for carefully chosen ranges. Those ranges follow a regular structure tied to the binary form of each index, so every entry in tree covers a short segment of the base array rather than a single position.
Most descriptions of Fenwick trees assume 1 based indexing. The base array is treated as if it had indices from 1 to n, and the tree array has size n + 1. Position 0 in tree stays unused. That convention matches the way binary representations behave, because the least significant set bit of the index tells the length of the range that tree[i] covers. With that convention, index arithmetic stays compact and works neatly with bit operations.
Prefix Sums In Fenwick Trees
Fenwick trees are built around prefix sums. For a base array arr[1..n], a prefix sum up to index i is arr[1] + arr[2] + ... + arr[i].
The tree does not store every prefix sum directly. Instead, each position i in the tree array stores the sum of a block of values that ends at index i. The length of that block equals the value of the least significant set bit in i, which is often written as lsb(i). With that rule, tree[i] holds the sum of the base values from arr[i - lsb(i) + 1] through arr[i]. Those blocks overlap in a controlled way, and together they provide enough information to recover any prefix sum with a short walk through the tree array.
For indices from 1 through 8, the layout looks like this when the tree is built with the usual rule. Index 1 in tree has binary form 001 and covers just arr[1]. Index 2 has binary form 010 and covers arr[1] through arr[2]. Index 3 has binary form 011 and covers only arr[3]. Index 4 has binary form 100 and covers arr[1] through arr[4]. Index 5 has binary form 101 and covers only arr[5]. Index 6 has binary form 110 and covers arr[5] through arr[6]. Index 7 has binary form 111 and covers only arr[7]. Index 8 has binary form 1000 and covers arr[1] through arr[8]. The blocks share some elements, but the way they are arranged makes it possible to pick a small set of them that add up to any prefix.
That description can feel a bit abstract on its own, so a small example helps. Suppose there is a base array with eight elements:
![long[] arr = {5, 2, 7, 3, 6, 1, 4, 2}; // treated as arr[1..8] long[] tree = new long[9]; // tree[0] unused, tree[1..8] filled below tree[1] = arr[0]; // covers [1, 1] tree[2] = arr[0] + arr[1]; // covers [1, 2] tree[3] = arr[2]; // covers [3, 3] tree[4] = arr[0] + arr[1] + arr[2] + arr[3]; // covers [1, 4] tree[5] = arr[4]; // covers [5, 5] tree[6] = arr[4] + arr[5]; // covers [5, 6] tree[7] = arr[6]; // covers [7, 7] tree[8] = arr[0] + arr[1] + arr[2] + arr[3] + arr[4] + arr[5] + arr[6] + arr[7]; // covers [1, 8]](https://substackcdn.com/image/fetch/$s_!ED9v!,f_auto,q_auto:good,fl_progressive:steep/https%3A%2F%2Fsubstack-post-media.s3.amazonaws.com%2Fpublic%2Fimages%2F9845bdca-c0bf-4874-90b0-bc0ccc074d09_1552x425.png "long[] arr = {5, 2, 7, 3, 6, 1, 4, 2}; // treated as arr[1..8] long[] tree = new long[9]; // tree[0] unused, tree[1..8] filled below tree[1] = arr[0]; // covers [1, 1] tree[2] = arr[0] + arr[1]; // covers [1, 2] tree[3] = arr[2]; // covers [3, 3] tree[4] = arr[0] + arr[1] + arr[2] + arr[3]; // covers [1, 4] tree[5] = arr[4]; // covers [5, 5] tree[6] = arr[4] + arr[5]; // covers [5, 6] tree[7] = arr[6]; // covers [7, 7] tree[8] = arr[0] + arr[1] + arr[2] + arr[3] + arr[4] + arr[5] + arr[6] + arr[7]; // covers [1, 8]")
This manual build follows the same rule that tree[i] stores a block ending at i whose length matches the least significant set bit of i. A real Fenwick tree would not hard code the sums in this way, but the result would match this layout after the structure had processed the same base values through its update routine.
From that layout, a prefix sum up to a given index can be broken down into a small collection of blocks from tree. Take a prefix up to index 6. The block at tree[6] covers arr[5] and arr[6]. The next block to the left that plugs the gap is tree[4], which covers arr[1] through arr[4]. Adding tree[6] and tree[4] gives the same result as summing arr[1] through arr[6] directly. That pair of indices 6 and 4 comes from subtracting the least significant set bit of 6 to reach 4, and then subtracting the least significant set bit of 4 to reach 0, which finishes the walk.
For a larger index, the walk uses more steps but still stays short. Think about index 13 in a bigger tree. The binary form of 13 is 1101. The least significant set bit has value 1, so the first block taken from tree[13] covers just arr[13]. Subtracting 1 from 13 yields 12, whose binary form is 1100. The least significant set bit there has value 4, so tree[12] covers arr[9] through arr[12]. Subtracting 4 gives 8, whose binary form is 1000, and tree[8] covers arr[1] through arr[8]. After subtracting 8, the index reaches 0 and the walk ends. The three blocks [1, 8], [9, 12], and [13, 13] together match the prefix from 1 through 13 with no gaps.
A small helper can print the covered segment for every index in a tree array, which is handy while learning this structure.
![private static int leastSignificantBit(int i) { return i & -i; } private static void printCoverage(int n) { for (int i = 1; i <= n; i++) { int span = leastSignificantBit(i); int from = i - span + 1; int to = i; System.out.println("tree[" + i + "] covers [" + from + ", " + to + "]"); } }](https://substackcdn.com/image/fetch/$s_!8mSE!,f_auto,q_auto:good,fl_progressive:steep/https%3A%2F%2Fsubstack-post-media.s3.amazonaws.com%2Fpublic%2Fimages%2F3146ac59-aebf-4c3a-8515-690f03c1a2fe_1555x425.png "private static int leastSignificantBit(int i) { return i & -i; } private static void printCoverage(int n) { for (int i = 1; i <= n; i++) { int span = leastSignificantBit(i); int from = i - span + 1; int to = i; System.out.println(\"tree[\" + i + \"] covers [\" + from + \", \" + to + \"]\"); } }")
Running printCoverage(8) with this code produces lines that match the segments described earlier, and seeing those ranges in the console helps tie the binary index rule to the base array segments.
The way the blocks are arranged in tree has a direct effect on performance. Every step in a prefix query clears one set bit in the current index, so the number of steps through the tree array cannot exceed the number of bits present in the initial index value. For an array of length n, that means at most about log2(n) iterations for each prefix sum, which gives a logarithmic bound on the work for both queries and updates built on these same index rules.
Least Significant Bit For Index Movement
The least significant set bit in an index drives more than just the length of the covered segment. It also controls how the code walks through the tree array during queries and updates. Reading and modifying tree entries boils down to repeatedly adding or subtracting that least significant bit, which makes the way indices move through the tree very regular.
In Java, the least significant set bit for a positive integer i can be extracted with a short method that relies on two’s complement arithmetic.
The value -i is the two’s complement negation of i. For a positive i, the bitwise and between i and -i produces a value that has exactly one bit set, and that bit is the lowest set bit in i. If i equals 6, its binary form is 110. The value -6 has low bits 010, so 6 & -6 yields 010, which has value 2. If i equals 12, its binary form is 1100. The value -12 has low bits 0100, so 12 & -12 yields 0100, which has value 4.
That least significant bit value plays two different parts for index movement. When code needs to move toward larger indices, it adds the least significant bit to the current index with i += lsb(i). When code needs to move toward smaller indices, it subtracts the least significant bit with i -= lsb(i). The same helper method supports both directions.
Take this basic utility method can report the range covered by any tree index by reading this bit and computing where the segment starts:
If segmentStart(6) is called, the method computes span = 2 and returns 5, which matches the earlier statement that tree[6] covers the interval from 5 to 6. For segmentStart(8), the method computes span = 8 and returns 1, which means tree[8] covers the interval from 1 to 8.
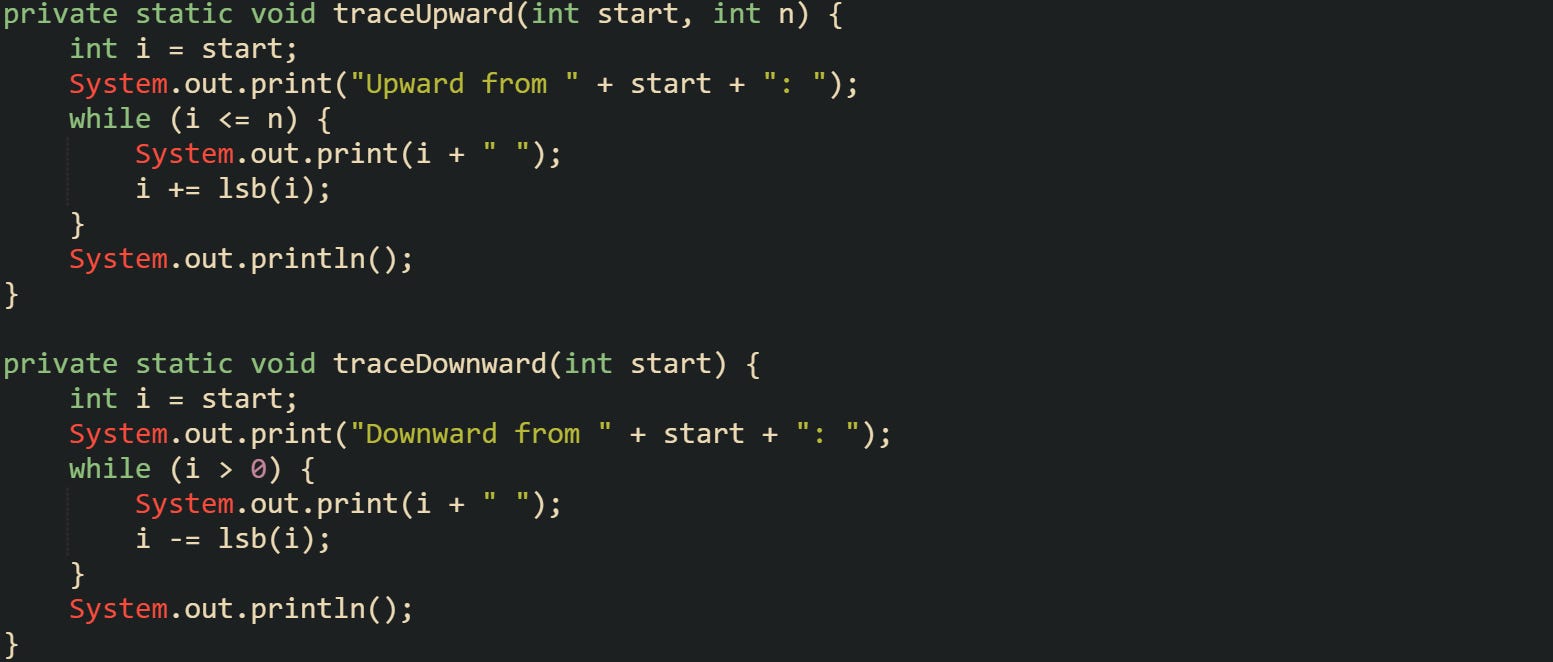
Index movement in a Fenwick tree follows a steady pattern. Movement toward the right, which is the direction used when propagating an update from a base index into the tree, repeatedly adds lsb(i) to i. That sequence of indices passes through every tree entry whose covered segment contains the original base index. Movement toward the left, which is the direction used when assembling a prefix sum, repeatedly subtracts lsb(i) from i. That sequence picks a set of blocks that exactly cover a prefix [1, i] without overlap.
To see the movement paths in a more solid way, a small trace routine helps:
Calling traceUpward(3, 8) prints the indices that would be touched by an update at base index 3 in an array of size 8, and calling traceDownward(13) prints the indices in the tree array that contribute to the prefix sum up to index 13. Those paths always terminate, because adding the least significant bit repeatedly pushes the index beyond n, and subtracting it repeatedly drives the index down to 0.
These short movement rules, all based on the same least significant bit helper, tie the layout of covered segments to the work that updates and queries perform, and they do it in a way that keeps the number of visited indices proportional to the number of bits in the current index value.
Fenwick Tree Operations
Fenwick trees support a small family of array operations that rely on the partial sums stored in the internal tree[] array. The central actions are point updates, where one base index changes by some delta, and prefix queries, where code asks for the sum from index 1 up to some index i. Range queries on [left, right] then follow from those same pieces, because a range sum is the difference between two prefix sums. Each of these operations touches only O(log n) entries in the internal array.
Point Updates Through Upward Propagation
Point updates add some offset to a single position in the logical base array. The value at that position changes, and every partial sum that depends on that value needs the same adjustment. Those partial sums live in tree[] at indices whose covered segments include the updated base index, so the update procedure has to visit exactly those entries and apply the delta.
The rule behind the update uses a short loop. Start at the 1 based index of the base element that changed, add the delta to tree[index], then move upward by adding the least significant set bit to the index. That jump lands on the next tree position whose stored segment still includes the original base index. Repeating this step walks through all entries that contain the updated value, and the loop finishes when the index passes n.
Take this common Java implementation that wraps this logic in a FenwickTree class that owns the internal array and its size:
![public final class FenwickTree { private final int size; private final long[] tree; public FenwickTree(int n) { this.size = n; this.tree = new long[n + 1]; // 1 based indexing, tree[0] unused } private static int lsb(int index) { return index & -index; } // add delta to base index (1-based) public void add(int index, long delta) { int i = index; while (i <= size) { tree[i] += delta; i += lsb(i); } } }](https://substackcdn.com/image/fetch/$s_!i9Bi!,f_auto,q_auto:good,fl_progressive:steep/https%3A%2F%2Fsubstack-post-media.s3.amazonaws.com%2Fpublic%2Fimages%2F66202aa1-95e5-497d-8196-965a9ab00ca2_1556x772.png "public final class FenwickTree { private final int size; private final long[] tree; public FenwickTree(int n) { this.size = n; this.tree = new long[n + 1]; // 1 based indexing, tree[0] unused } private static int lsb(int index) { return index & -index; } // add delta to base index (1-based) public void add(int index, long delta) { int i = index; while (i <= size) { tree[i] += delta; i += lsb(i); } } }")
This class treats the caller’s data as a logical base array with indices from 1 through size. The add method updates all stored partial sums that depend on the adjusted base value. The method touches at most one tree entry for each bit present in the indices visited in the loop, so the work stays proportional to the logarithm of the array length.
Lots of callers start with an existing array of values and want a Fenwick tree that already reflects those values. One direct path is to process each element as a point update through the same add method, which keeps the internal logic in one place.
![public static FenwickTree fromArray(long[] values) { int n = values.length; FenwickTree ft = new FenwickTree(n); for (int i = 0; i < n; i++) { int baseIndex = i + 1; // map 0-based position to 1-based long delta = values[i]; ft.add(baseIndex, delta); } return ft; }](https://substackcdn.com/image/fetch/$s_!xpQ9!,f_auto,q_auto:good,fl_progressive:steep/https%3A%2F%2Fsubstack-post-media.s3.amazonaws.com%2Fpublic%2Fimages%2F3ec745bd-bd7c-4020-baa6-782506510560_1556x348.png "public static FenwickTree fromArray(long[] values) { int n = values.length; FenwickTree ft = new FenwickTree(n); for (int i = 0; i < n; i++) { int baseIndex = i + 1; // map 0-based position to 1-based long delta = values[i]; ft.add(baseIndex, delta); } return ft; }")
This build method treats the input values array as a zero based view of arr[1..n] and feeds each element into the tree through add. The cost of construction through this route grows on the order of n log n, because each call to add updates O(log n) partial sums.
Prefix Sum Queries Through Downward Traversal
Prefix sum queries ask for the sum of all base values from index 1 through some index i. The Fenwick tree does not store that full prefix in a single cell. Instead, it stores sums for a family of segments whose lengths are powers of two and whose right endpoints match the array indices. A prefix query reconstructs the desired sum from a small group of these stored segments. The reconstruction again follows the binary structure of the index. Starting from i, the query logic adds tree[i] to a running total, then moves left by subtracting the least significant set bit from the index. Each step removes one set bit from the binary form of the index and lands on the next partial sum that covers the remaining part of the prefix. The traversal stops when the index reaches zero, at which point the running total holds the full prefix sum.
Inside the same FenwickTree class, the prefix operation sits naturally beside the update method.
![public long prefixSum(int index) { long acc = 0L; int i = index; while (i > 0) { acc += tree[i]; i -= lsb(i); } return acc; }](https://substackcdn.com/image/fetch/$s_!ccOh!,f_auto,q_auto:good,fl_progressive:steep/https%3A%2F%2Fsubstack-post-media.s3.amazonaws.com%2Fpublic%2Fimages%2Feeff62d4-c87d-4d72-a85a-18b82ecfc0b5_1554x318.png "public long prefixSum(int index) { long acc = 0L; int i = index; while (i > 0) { acc += tree[i]; i -= lsb(i); } return acc; }")
This method returns the sum arr[1] + arr[2] + ... + arr[index] for the logical base array. The loop visits at most one index for each set bit in the original index value, and the number of bits for indices up to size grows on the order of log2(size), so the running time is logarithmic in the array length.
Client code calls prefixSum much like any other query on an indexed data structure, with the difference that the index passed to prefixSum follows the 1 based convention.
![public static void main(String[] args) { long[] values = {3, 1, 4, 2, 7}; FenwickTree ft = FenwickTree.fromArray(values); long firstThree = ft.prefixSum(3); // 3 + 1 + 4 = 8 long firstFour = ft.prefixSum(4); // 3 + 1 + 4 + 2 = 10 System.out.println("Prefix up to 3 = " + firstThree); System.out.println("Prefix up to 4 = " + firstFour); }](https://substackcdn.com/image/fetch/$s_!2Qax!,f_auto,q_auto:good,fl_progressive:steep/https%3A%2F%2Fsubstack-post-media.s3.amazonaws.com%2Fpublic%2Fimages%2Feddbc644-4596-4c0d-b971-6ea5afd76c54_1556x354.png "public static void main(String[] args) { long[] values = {3, 1, 4, 2, 7}; FenwickTree ft = FenwickTree.fromArray(values); long firstThree = ft.prefixSum(3); // 3 + 1 + 4 = 8 long firstFour = ft.prefixSum(4); // 3 + 1 + 4 + 2 = 10 System.out.println(\"Prefix up to 3 = \" + firstThree); System.out.println(\"Prefix up to 4 = \" + firstFour); }")
This small main method treats the values array as a sequence of five numbers and asks for the sum of the first three and first four elements through prefixSum. Both queries run in logarithmic time, and the results match what a direct loop over the base values would compute.
Range Queries Built From Prefix Sums
Range queries ask for sums on subarrays [left, right] within the base data. A Fenwick tree handles these queries by expressing the range sum as the difference between two prefix sums. For indices with 1 <= left <= right, the identity sum(left..right) = prefix(right) - prefix(left - 1) holds for any sequence of numbers. The tree supplies an efficient way to obtain each prefix sum, so the range sum inherits the same logarithmic cost as two separate prefix calls.
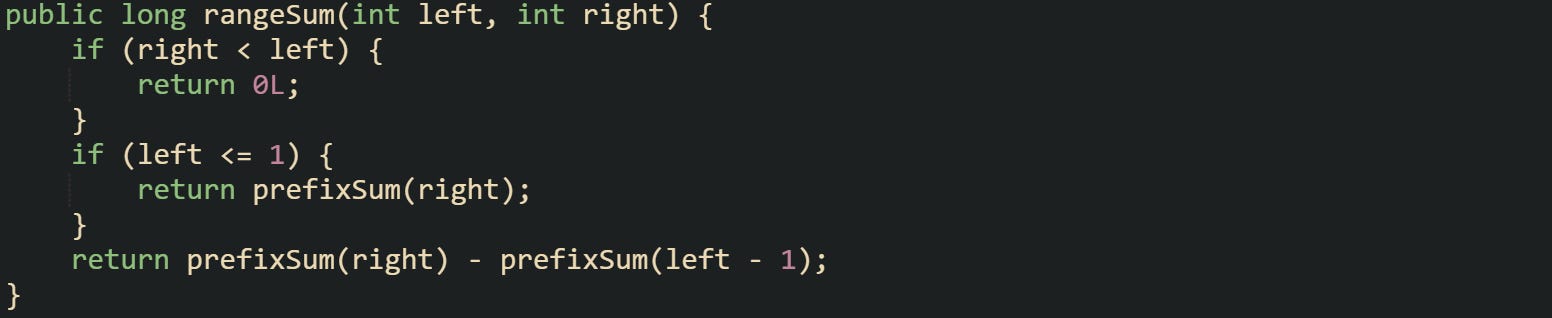
A common implementation adds a helper that wraps this identity and handles boundary cases in a single place. That helper relies on the existing prefixSum method, so no direct access to the internal tree[] array is needed.
This method returns zero for an invalid range where right is less than left. For ranges that begin at index 1, it falls back to a single prefix sum. For general ranges, it subtracts the prefix up to left - 1 from the prefix up to right. Each call performs at most two prefix operations, so the complexity stays within a constant factor of O(log n).
Range sums are especially useful with arrays that represent cumulative quantities such as counts or totals. Daily measurements make a straightforward example of how this works in practice visually:
![long[] sales = {120, 150, 130, 160, 200, 180, 140}; FenwickTree ft = FenwickTree.fromArray(sales); // total from day 2 through day 5 long midWeek = ft.rangeSum(2, 5); // total for the whole week long fullWeek = ft.rangeSum(1, 7); System.out.println("Days 2-5 total = " + midWeek); System.out.println("Full week total = " + fullWeek);](https://substackcdn.com/image/fetch/$s_!tiCT!,f_auto,q_auto:good,fl_progressive:steep/https%3A%2F%2Fsubstack-post-media.s3.amazonaws.com%2Fpublic%2Fimages%2F3f814e0a-0386-4181-8b39-d6c29bd68f92_1560x388.png "long[] sales = {120, 150, 130, 160, 200, 180, 140}; FenwickTree ft = FenwickTree.fromArray(sales); // total from day 2 through day 5 long midWeek = ft.rangeSum(2, 5); // total for the whole week long fullWeek = ft.rangeSum(1, 7); System.out.println(\"Days 2-5 total = \" + midWeek); System.out.println(\"Full week total = \" + fullWeek);")
The rangeSum method in this example treats the sales array as a record of daily values and answers questions about segments inside that record. Each query, whether it covers a short portion or the full array, still runs in logarithmic time because it reuses the same prefix logic that the tree already provides.
Conclusion
Fenwick trees in Java rely on a compact array of partial sums, a consistent 1 based index layout, and least significant bit arithmetic to control how updates and queries move through the structure. Point changes at a base index travel upward through the internal array by repeated index jumps, touching exactly those entries whose stored segments include the changed value, while prefix queries move downward by peeling off one binary segment at a time. Range sums then fall out from differences of prefix sums, so a single set of mechanics handles updates, prefixes, and subarray queries with logarithmic work and a small memory footprint.