Interval Merging Logic in Java

Image Source

Working with interval merging in Java lets you pull overlapping ranges into a compact set, so later parts of the code deal with fewer intervals and less clutter. Schedules, booking systems, and geometry problems tend to use ranges with a start value and an end value, and raw input can arrive with overlaps and gaps in any order. Sorting the intervals by start value turns that scattered input into an ordered sequence where possible overlaps sit next to each other, and a single linear pass then merges everything into a non-overlapping set of ranges.

Sorting Interval Data For Merging

Typically, dealing with interval lists gets easier if the data already sits in a predictable order. Intervals that come in from clients or files tend to arrive in any sequence the producer happened to choose, which means overlapping ranges can appear far apart from one another. Sorting by the start value reshapes that jumble into a run of intervals where any candidate overlaps sit next to each other. After that, a merge step can walk from left to right without jumping around or rechecking earlier entries.

Sorting only pays off when every interval has a stable, well defined internal layout. Start and end values need a fixed meaning, and callers need to agree on how those values relate to the actual range of data or time they stand for. After that contract is in place, sort code can focus purely on numeric comparisons without worrying about hidden conventions.

Fixed Interval Representation In Java

Code needs a stable way to hold a start and an end before any sort can do its work. One common layout in Java uses a small class with two fields, one for the start point and one for the end point. That matches many interview problems and also maps well to normal business ranges such as price tiers or booked time blocks.

This version treats both endpoints as inclusive, so an instance with start equal to 2 and end equal to 5 covers integer points 2, 3, 4, and 5. Many time based APIs instead follow a half open style, where a range [start, end) includes start and excludes end. Both conventions work as long as they stay consistent across code that creates intervals, sorts them, and later merges them.

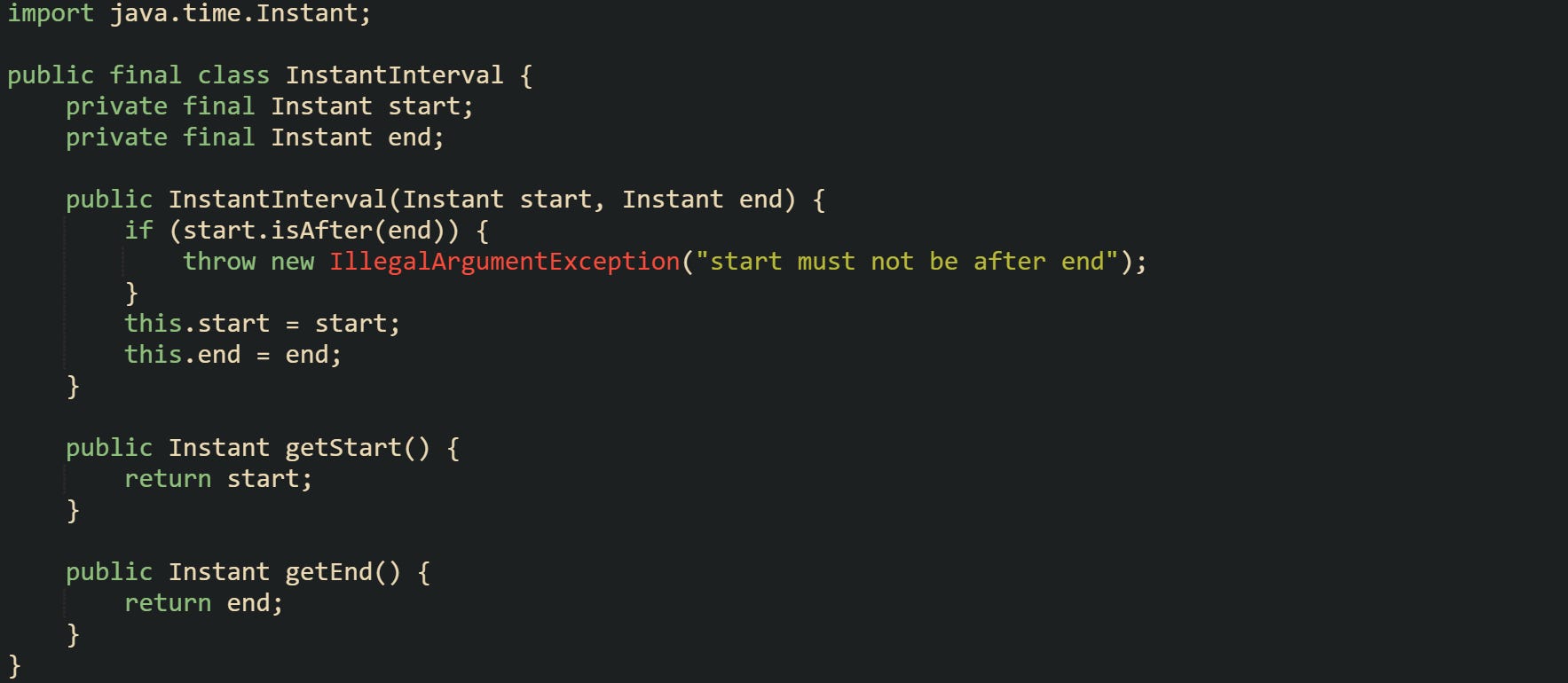
Projects that track time ranges often move beyond plain integers and store LocalDateTime or Instant values instead. The same idea still applies, only the field types change:

Generic code that operates on both numeric intervals and time based intervals tends to rely on methods like getStart and getEnd, so having that pair of accessors makes it easier to plug into utility methods.

Java also offers records, which give a compact way to define the same data carrier. Some developers prefer using records for plain data holders because the compiler generates accessors and toString for them.

Validation inside the record compact constructor keeps the guarantee that start never exceeds end. Merge and sort logic can then work with Range instances without repeatedly checking that invariant.

There is also a different style that drops the named type and uses arrays of two integers. This layout matches many interval examples in algorithm textbooks and blogs, and it keeps a stable contract as long as index 0 always holds the start value and index 1 always holds the end value.

Array based representations work well for short lived data such as input for a single operation, while named types like Interval or Range are often better when ranges move across layers of an application. No matter which storage style fits a project, the sort logic that we will go over next still reads the first value as the start point and the second value as the end point.

Sorting Intervals By Start Position

Lots of bugs in merge logic show up when code tries to reason about overlaps while the data still sits in random order. Sorting by start value gives a strong guarantee about how intervals appear in the list. Every interval that starts later appears at or after the position of one that starts earlier. That simple fact makes it safe to focus on neighbors when checking for overlaps.

With the object based Interval class, a comparator on the start field captures the sort rule in a single place, like this:

Intervals in the printed result come out ordered by their start point, even though the input list added them in a different sequence. The list now places every possible overlap candidate next to the ranges it could intersect with.

Sometimes a project wants intervals that share a starting point to appear in a predictable secondary order. Sorting by start first and end second gives that behavior:

Shorter intervals that begin at the same point then appear ahead of longer ones. Merge logic usually does not depend on that secondary rule, but human readers of logs or debug output may find it easier to track.

Array based intervals follow the same ideas with Arrays.sort and a custom comparator. Think of each int[] as a two element record where index 0 holds the start and index 1 holds the end:

After this call to Arrays.sort, any interval that appears later in the array has a start value that is greater than or equal to the start value of every interval that came before. That single property drives the accuracy of the later merge scan.

Sorting work itself grows with the number of intervals n. Common implementations of List.sort and Arrays.sort for object data rely on algorithms that run in time on the order of n log n. For interval merging, that cost normally dominates the total runtime because the subsequent scan over the sorted list only walks the data once from left to right.

Ordering by the start value also shapes how we think about gaps. Take three intervals i, j, and k with j in the middle after sorting. If j starts after i ends, there is a gap between them. Any interval k that appears after j starts at least as late as j, so k also starts after the end of i. That argument means no later interval can ever overlap i once the algorithm has reached an interval that starts to the right of i and does not intersect it.

Merging Intervals

After sorting, merge code walks through the list and builds a new list of non-overlapping ranges. At each step, only two intervals matter in that walk, the current merged range that collects everything seen so far and the next interval pulled from the sorted list. Sorting by start value guarantees that any overlap that still needs to be handled must involve those two ranges, so the algorithm never has to jump backward or scan ahead to search for hidden overlaps.

When you read the merge loop, it helps to visualize a sweep from left to right across a number line. The sweep carries a single active range that grows as long as new intervals touch or overlap it. As soon as an interval appears that starts strictly after the end of the active range, that active range gets stored in the output and a new one begins at the position of the fresh interval.

Sequential Scan Over Sorted Intervals

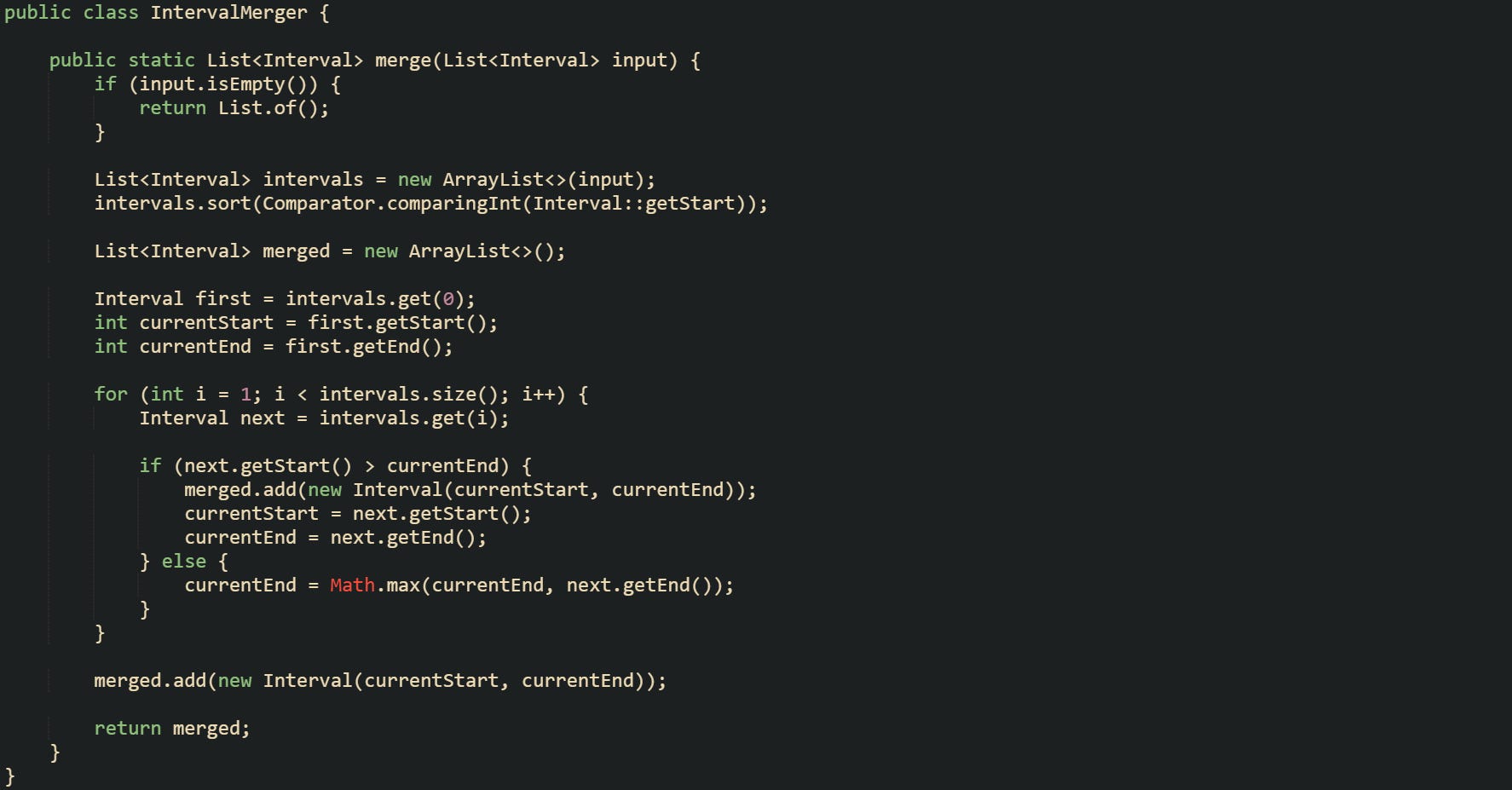
Many merge routines start by copying the input, sorting that copy by start value, and then scanning from index 0 up to the end. For a class based representation like Interval, a merge method usually starts from the first interval and treats that as the initial merged range.

Logic inside the loop works with just a few values, yet it tracks all intervals processed so far. Variables currentStart and currentEnd mark the smallest start and the largest end among every interval that has been folded into the active merged range. Every new interval is either absorbed into that active range through the Math.max call or triggers a flush when a gap appears.

Let’s take a look at a run with input and output together, a short main method can help make the flow a bit more visible:

Starting from unsorted input, the call to merge first sorts by start value, then performs a single linear pass through that sorted list. The first three intervals produce [1, 8] because every new interval touches or overlaps the current merged range. The last interval [10, 12] starts after the end of that merged range, so it becomes a second entry in the output.

Array based input follows the same idea, only the data holder changes. Intervals stored as int[][] can be merged with one pass as well, as long as index 0 holds start and index 1 holds end.

Both class based and array based versions share the same structure. An active merged range is tracked by two integers, new intervals arrive in sorted start order, and each interval either closes out the current merged range or gets absorbed into it by extending currentEnd.

Overlap Conditions With Range Growth

Checks for overlap sit at the heart of the merge loop. For integer ranges that treat both ends as inclusive, two intervals intersect whenever the later one starts at or before the end of the earlier one. With sorted data, the second interval in that comparison always has a start value greater than or equal to the start of the first, so only one inequality remains.

Think of two inclusive intervals [aStart, aEnd] and [bStart, bEnd] that appear in sorted order. If bStart <= aEnd, there is at least one integer point that both intervals share. If bStart > aEnd, the intervals sit apart with a gap between them. That exact logic appears in the merge loop through the test nextStart > currentEnd for a gap and the else block for overlap or contact.

plenty of projects prefer half open ranges [start, end) for index based ranges and time windows. With that convention, a point equal to end lies just after the range. Two half open ranges touch without overlapping when one ends exactly where the next one starts. That small difference in meaning changes how the comparison should work.

Take this helper method:

Inclusive ranges treat shared endpoints as overlap, while half open ranges treat shared endpoints as contact without shared content. When intervals arrive pre-sorted and the merge loop always compares the current merged range with the next one in order, those helpers reduce to single comparisons against currentEnd, but it helps to see the full expressions first.

Inclusive integer intervals like [1, 3] and [3, 5] share the point 3, so that is overlap, not “touching without overlap.” Boundary contact without shared content shows up with half-open ranges [start, end) or with continuous ranges where endpoints can meet without sharing a point. For inclusive integer ranges, a common business choice is whether to also merge adjacency like [1, 3] and [4, 5]. That changes the gap test like this:

The choice of comparison controls how the merge treats boundary cases such as shared endpoints in [start, end] and boundary contact in [start, end), so the output either collapses those cases into one interval or keeps them as separate entries. The rest of the merge loop stays unchanged.

Growth of the merged range always happens on the right edge. Sorted input guarantees that no future interval can start before currentStart. That fact lets the algorithm hold currentStart constant while calling Math.max on the end point to bring the merged range up to date.

Seeing a short example might help, so take sorted intervals [1, 4], [2, 5], [7, 8], and [8, 10] with inclusive endpoints and a comparison that treats touching ranges as merged:

First interval creates an active range [1, 4]. Second interval starts at 2, which is not greater than 4, so it overlaps, and currentEnd becomes max(4, 5) which equals 5. Third interval starts at 7, which is greater than 5, so [1, 5] moves into the output and the active range resets to [7, 8]. Fourth interval touches that active range at 8, so currentEnd becomes max(8, 10) which equals 10. Final output holds [1, 5] and [7, 10].

Time Cost Versus Memory Use

Runtime analysis for interval merging breaks naturally into two stages. Sorting dominates the first stage, and a linear pass takes care of the second. For n intervals, common sorting algorithms in List.sort and Arrays.sort for object data run in time proportional to n log n. That sorting stage sets up the strong ordering property that the scan relies on. The scan then visits each interval exactly once, doing constant work per interval, which leads to linear time in n for that second stage.

Extra memory use depends on how the code stores results and how much it alters the input. Earlier examples allocate a new list of merged intervals and leave the original list untouched. That style keeps method boundaries easier to reason about, because callers never see their original data modified under their feet, and garbage collection reclaims intermediate lists when they fall out of scope.

Some scenarios favor tighter control over memory and allow in place merging. With array based input, merged ranges can be written back into the front part of the array while scanning. That layout keeps all ranges in a single int[][] buffer. For example, index writeIndex tracks where the next merged result should land, and index i tracks the next input interval to read:

The total number of element reads and writes stays proportional to the number of intervals. Sorting still costs n log n, and the merge pass stays linear. Extra memory beyond the input array is limited to a few index variables and the trailing Arrays.copyOf call that trims the array down to the final number of merged ranges.

Conclusion

Interval merging in Java boils down to three parts, a stable representation for start and end points, a sort by start value, and a single scan that either extends the current range or flushes it when a gap appears. With that structure in place, the same mechanics work for numeric ranges, time windows, and booking slots, and the cost stays easy to reason about, with sorting at n log n time and the merge pass at linear time.

1. Java Collections Framework Documentation

2. Comparator Interface Java SE Documentation

3. Arrays Utility Class Java SE Documentation

4. Instant Class Java SE Documentation