Kadane's Algorithm for Maximum Subarray in Java

Image Source

Locating the subarray with the largest sum in a list of integers has become a frequently encountered topic for coding interviews and practical software work. The idea is to work through an array that may hold both positive and negative values and figure out which continuous stretch adds up to the greatest total. Kadane’s Algorithm handles that efficiently by moving through the array only once, adjusting running sums as it goes. It’s a method that balances performance and clarity while staying accurate around edge cases like all-negative arrays or integer overflow.

How Kadane’s Algorithm Finds the Maximum Subarray

Kadane’s Algorithm has earned its place in computer science because it manages to uncover the largest contiguous sum in a list of numbers without checking every possible combination. It doesn’t need extra data structures or nested loops; it simply walks through the array once, carrying forward a running total and keeping track of the best result along the way. The strength of the algorithm comes from how it decides when to reset the running total and when to keep going. That balance lets it handle arrays with both gains and losses, positive and negative numbers, while staying fast enough for real-world data sizes.

The Logic Behind Dynamic Summation

At the heart of Kadane’s Algorithm is a decision that happens at every element: should the current number be added to the existing total, or should the algorithm start fresh from that number? That single choice determines the efficiency of the result. When the cumulative sum up to that point becomes smaller than the current value itself, it’s better to restart, as adding the previous total would only reduce the next sum.

A compact version of the algorithm in Java looks like this:

This code reveals how the algorithm moves through the array while continuously updating two values: currentSum tracks the total for the ongoing subarray, while maxSum keeps record of the best total so far. When currentSum drops below the current element, the logic resets, cutting away dead weight from the running sum.

That update pattern means Kadane’s Algorithm can respond to changes in sign quickly. A sequence that dips into negatives doesn’t cause failure, it just provides an opportunity to start again from a more favorable point. This local decision-making gives the algorithm its strength without adding unnecessary loops or memory overhead.

To make that behavior easier to see, here’s a trace version that logs each decision step by step:

This second version helps visualize how currentSum changes after each comparison and how the algorithm naturally “forgets” poor totals. It’s this continuous decision-making that gives Kadane’s Algorithm its fluid efficiency.

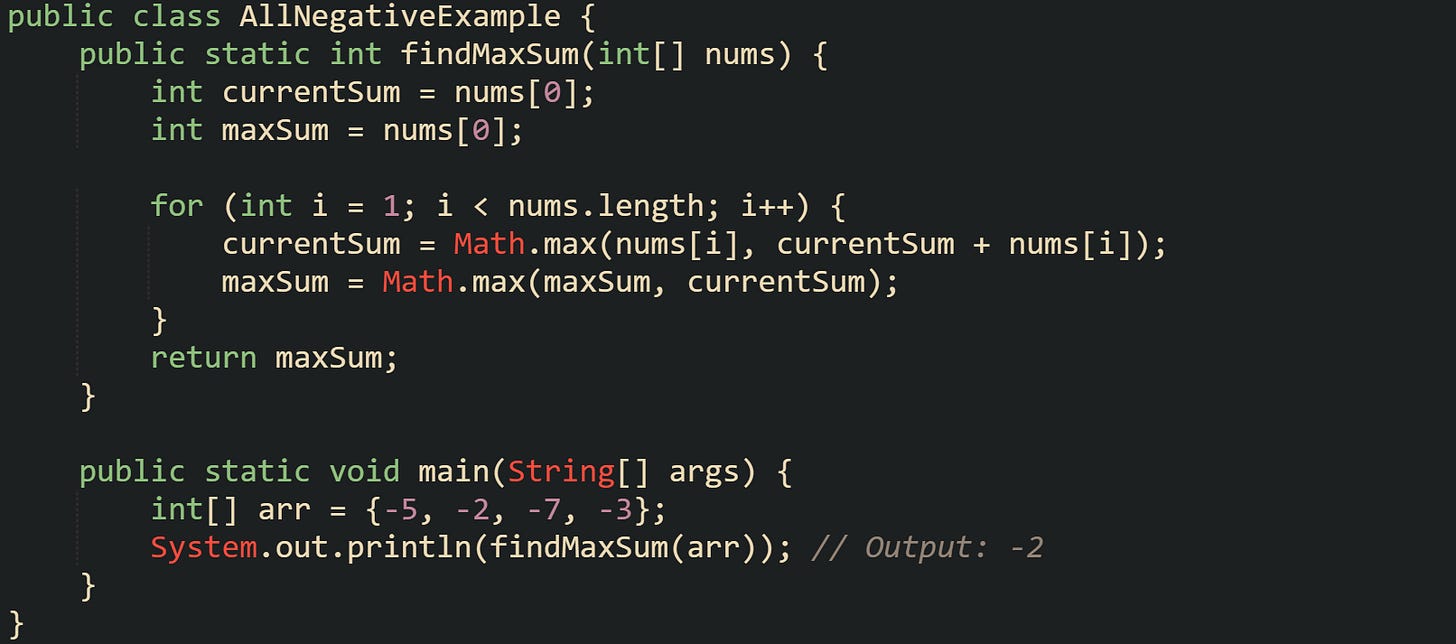
Edge Handling for All-Negative Arrays

Many arrays in real scenarios contain negative values throughout, which can break a naive version of Kadane’s Algorithm that resets current sums to zero. If every value is negative, zero is not a valid answer, because the algorithm must still pick one continuous range. To avoid this, both the maximum and current sums are initialized to the first element of the array rather than zero. That small change makes all the difference.

That logic makes sure that the algorithm doesn’t discard valid negative sums in favor of zero. It also gives reliable behavior for short datasets by grounding the initial comparison in real input values and for an empty array, handle it explicitly before calling the method.

For more visualization, take the array [-5, -2, -7, -3]. If the algorithm started with zero as its base, it would return zero, which doesn’t exist in the array. But with the initialization set to the first element, it correctly identifies -2 as the largest sum possible. This behavior matters in domains like signal processing or error tracking, where even the least-negative streak might represent the best outcome available.

Through these small but deliberate rules, Kadane’s Algorithm keeps its accuracy across every type of array, from all-positive to all-negative, while remaining true to its one-pass efficiency.

Extending Kadane’s Algorithm for Practical Scenarios

Kadane’s Algorithm is most known for handling one-dimensional arrays, but its structure can be adapted for different data types, larger ranges, and even multidimensional problems. It also fits real-world use cases where identifying a maximum sequence is more valuable when paired with location data or timing. The same principle of updating dynamic sums continues to serve as the base logic, but the implementation can grow to handle more practical conditions, from financial tracking to data analytics.

Tracking the Subarray Indices

Knowing the sum alone sometimes isn’t enough. Many use cases benefit from finding where that subarray starts and ends, especially when analyzing data streams, request traffic, or stock values. The expanded version of Kadane’s Algorithm tracks both the indices and the sum, allowing developers to pinpoint exactly which range contributes to the maximum outcome.

This version keeps two start markers, one temporary and one final, to help detect when a new sequence overtakes the old one. The ability to see both the indices and the total can help track a profitable streak or an anomaly range without extra computations.

To take it one step further, it can be modified to also return the subarray itself, which can be helpful for data visualization or result comparison.

This additional step makes Kadane’s logic more practical for production analytics where understanding the actual segment, not just its sum, is necessary.

Handling Overflow with Larger Data

Kadane’s Algorithm relies on cumulative sums, which can grow large when dealing with high-value data like financial records, scientific readings, or extended time series. Integer overflow becomes a concern when sums exceed the 32-bit integer range. To prevent silent corruption of values, converting the sums to use Java’s long type keeps the calculations safe.

That adjustment keeps the logic intact but safeguards the integrity of results. Overflow isn’t always obvious until it distorts totals, which can happen quickly with long datasets. Switching to long makes sure larger inputs can still be processed without losing precision.

Sometimes, the dataset might mix positive and negative floating-point numbers, such as when tracking gradual changes like sensor readings. Kadane’s Algorithm still holds up under these conditions, though using double introduces a new challenge, tiny rounding errors. When high precision is required, rounding results manually or with libraries like BigDecimal prevents drift across iterations.

That version offers the same logic as the integer form but supports precise calculations where even small decimal deviations matter.

Extending to Two-Dimensional Arrays

Kadane’s principle doesn’t stop with one-dimensional lists. It can also find the submatrix with the largest sum inside a two-dimensional grid, which is useful in problems involving image brightness, heat maps, or transaction clusters. The idea is to compress rows temporarily into a one-dimensional array, apply Kadane’s Algorithm, and then repeat this process while changing the top and bottom boundaries.

The nested structure increases time complexity to O(n³), but the method stays effective for grids of practical size.

In this version, every row boundary acts as a layer that merges column sums into a temporary array. Kadane’s one-dimensional logic runs over that array to find the most favorable column band. Stacking that across row pairs allows it to identify the best rectangular region in the matrix.

This form has proven useful in data heatmaps or geospatial data, where values represent density or frequency. It adapts Kadane’s iterative logic to a wider dimension without losing its foundation.

Integration with Real Applications

Kadane’s Algorithm finds its place in various domains that rely on detecting streaks of strong performance or identifying problematic dips. The algorithm’s mechanics fit naturally into areas like finance, analytics, and even performance tracking.

In finance, it helps detect a period of maximum profit in fluctuating stock prices. Analysts can use it to find the most profitable buy-sell window within a single day’s timeline. In signal processing or time-series analysis, it identifies stretches of high activity. And in server load data, it helps pinpoint peaks that need scaling attention.

Here’s a small example using a stock-like dataset to find the strongest growth streak:

That implementation can be embedded in larger systems where periodic evaluations run automatically. It scales easily to large datasets because its O(n) complexity keeps performance linear.

Some developers extend the concept further for streaming inputs. In streaming environments, Kadane’s logic is applied incrementally as new data points arrive, making it practical for live dashboards or analytics tools. The running totals are continuously updated, and only a few variables are retained in memory.

That kind of streaming-friendly use keeps Kadane’s Algorithm relevant in modern event-driven systems, where real-time feedback matters. It works quietly behind the scenes, evaluating sums continuously without storing an entire dataset, which makes it fit naturally into monitoring tools and financial engines alike.

Conclusion

Kadane’s Algorithm stands out for how naturally it turns a simple idea into an efficient process. Its mechanics rely on real-time decisions that track running totals, drop weak sums, and capture the best streak in a single pass. That same balance of reset and carry-forward logic lets it scale from small lists to large datasets and even multi-dimensional grids. It continues to serve as one of the clearest examples of how thoughtful iteration and dynamic sums can uncover the strongest continuous range without excess computation.

1. Java Math Class Documentation

2. Java Arrays Class Documentation

3. BigDecimal Class Documentation

4. Oracle Java Tutorials on Arrays