LeetCode #1: Two Sum — Solved in Java

Brute Force and Hash Map Solutions

Image Source

Two Sum is one of the most well-known problems on LeetCode. It was the first one I ever solved, and it comes up often in interviews too. The two solutions below are written in Java and can be copied straight into the LeetCode editor without any changes. We’ll go through each one step by step so you can see exactly how they work. You’ll find the copy-paste versions of both at the very end.

Given an array of integers nums and an integer target, return indices of the two numbers such that they add up to target.

You may assume that each input would have exactly one solution, and you may not use the same element twice.

You can return the answer in any order.

Examples:

• Input: nums = [2, 7, 11, 15], target = 9
  Output: [0, 1]
  Explanation: nums[0] + nums[1] == 9, so we return [0, 1]

• Input: nums = [3, 2, 4], target = 6
  Output: [1, 2]

• Input: nums = [3, 3], target = 6
  Output: [0, 1]

Constraints:

• 2 <= nums.length <= 10⁴

• -10⁹ <= nums[i], target <= 10⁹

• Only one valid answer exists.

Solution 1 — Brute Force (O(n²))

This version checks every pair of numbers in the array to see if any two of them add up to the target. It's not the fastest method, but it’s easy to follow and works reliably for smaller inputs.

Let’s walk through it piece by piece:

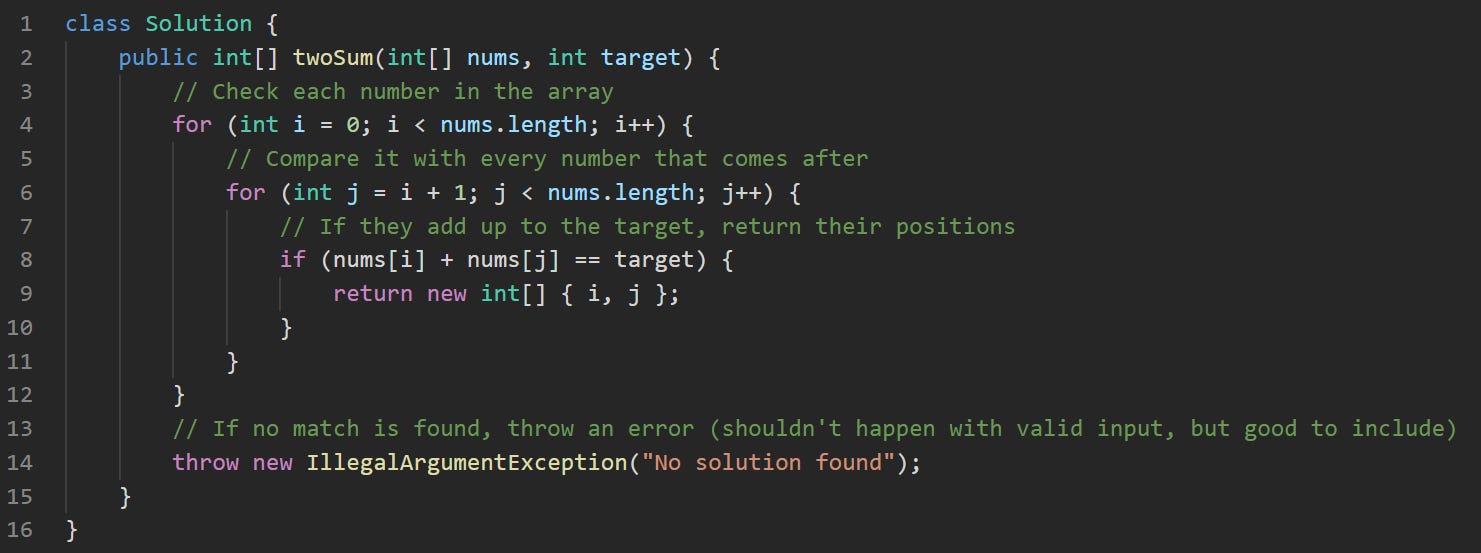
class Solution {

This line defines the class that LeetCode expects. It’s just a wrapper, and you don’t need to touch it.

public int[] twoSum(int[] nums, int target) {

Here we define a method called twoSum. It takes an array of integers called nums and a single integer called target. It’s going to return an array containing the two indices of the numbers that add up to that target.

for (int i = 0; i < nums.length; i++) {

This outer loop starts at the beginning of the array and moves forward one number at a time. The variable i is the index of the first number we’re trying out.

for (int j = i + 1; j < nums.length; j++) {

Inside the first loop, this second loop goes through the rest of the array, starting just after i. This way, we don’t check the same pair twice, and we don’t pair a number with itself.

if (nums[i] + nums[j] == target) {

Now we add the two numbers together. We're adding nums[i] and nums[j]. If the result equals the target, we’ve found the solution.

return new int[] { i, j };

If the condition is true, we return the indices right away. That’s the answer the problem wants.

                }
            }
        }

These just close the loops. If the correct pair is found, we’ll never reach the end because the method already returned.

throw new IllegalArgumentException("No solution found");

This is a fallback. The problem guarantees one solution, so this line should never run. But it's good to include a safety net like this just in case the input isn’t what you expected.

The time cost grows fast as the array gets longer, which puts it at O(n²) in the worst case. On the other hand, it doesn't use any extra memory beyond a couple of variables, so the space usage stays at O(1).

Solution 2 — Hash Map (O(n))

This version solves the problem by remembering the numbers we've already seen and checking each new number against them. It’s much faster than the brute force version, especially with bigger arrays.

Let’s break it down step by step:

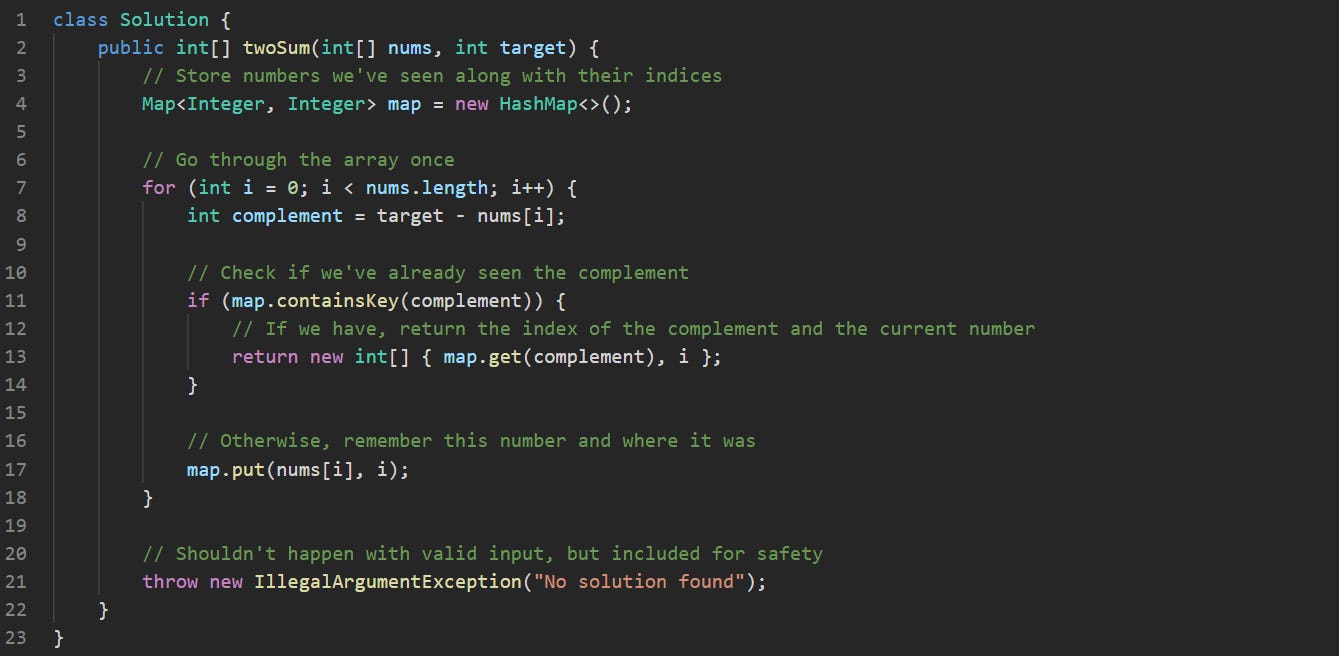
class Solution {

This starts the class definition. Nothing you need to change here. It's part of the structure LeetCode expects.

public int[] twoSum(int[] nums, int target) {

We define a method called twoSum that takes an array of numbers and a target sum. Like before, it returns an array with the two indices that add up to that target.

Map<Integer, Integer> map = new HashMap<>();

Here we create a new hash map. This map will hold each number we've seen so far, using the number as the key and its index as the value. That way, we can check later if the number we’re looking for is already there.

for (int i = 0; i < nums.length; i++) {

We loop through the array one number at a time. The index i tells us where we are in the array.

int complement = target - nums[i];

This line figures out what number would need to pair with nums[i] to make the target. That number is called the complement.

if (map.containsKey(complement)) {

We check if that complement is already in the map. If it is, that means we've seen the number we need, and we know its index.

return new int[] { map.get(complement), i };

If we found a match, we return the index of the complement (which we stored earlier) and the current index. That’s our answer.

map.put(nums[i], i);

We add the current number to the map, using the number as the key and its index as the value. Now it’s available for the next checks that come after this point.

throw new IllegalArgumentException("No solution found");

Just like the first solution, this is a backup in case something goes wrong. The problem says there will always be a valid answer, so this line shouldn’t run.

This version finishes the job in a single loop. Every number is only processed once, which gives it O(n) time complexity. It does use extra memory to keep track of what’s already been seen, so space complexity is also O(n). The reason it works so fast is because hash maps let you check if a value exists without looping through the entries. They use a hash function to jump directly to the spot where the value should be. That’s what makes this method useful in coding interviews. It cuts down the work while still giving a clear, readable solution.

Brute Force Version — Copy and Paste

class Solution {
    public int[] twoSum(int[] nums, int target) {
        for (int i = 0; i < nums.length; i++) {
            for (int j = i + 1; j < nums.length; j++) {
                if (nums[i] + nums[j] == target) {
                    return new int[] { i, j };
                }
            }
        }
        throw new IllegalArgumentException("No solution found");
    }
}

Hash Map Version — Copy and Paste

class Solution {
    public int[] twoSum(int[] nums, int target) {
        Map<Integer, Integer> map = new HashMap<>();

        for (int i = 0; i < nums.length; i++) {
            int complement = target - nums[i];

            if (map.containsKey(complement)) {
                return new int[] { map.get(complement), i };
            }

            map.put(nums[i], i);
        }

        throw new IllegalArgumentException("No solution found");
    }
}