LeetCode #10: Regular Expression Matching — Solved in Java

Recursive Match with Conditions and Dynamic Programming with a 2D Table

Image Source

This problem asks you to match a string against a pattern that may include two special characters: . and *. The dot matches any single character, while the asterisk means zero or more of the character that came just before it. The match has to account for the full string, not just part of it.

We will start with a basic recursive version that follows the logic as described. Then we’ll move on to a version that uses dynamic programming to cut down on repeated work. Both versions are broken down step by step, and the final code is ready to copy and run at the end.

LeetCode: Regular Expression Matching

Given an input string s and a pattern p, implement regular expression matching with support for '.' and '*' where:

• '.' Matches any single character.​​​​

• '*' Matches zero or more of the preceding element.

The matching should cover the entire input string (not partial).

Example 1:

• Input: s = "aa", p = "a"

  Output: false

  Explanation: "a" does not match the entire string "aa".

Example 2:

• Input: s = "aa", p = "a*"

  Output: true

  Explanation: '*' means zero or more of the preceding element, 'a'. Therefore, by repeating 'a' once, it becomes "aa".

Example 3:

• Input: s = "ab", p = ".*"

  Output: true

  Explanation: ".*" means "zero or more (*) of any character (.)".

Constraints:

• 1 <= s.length <= 20

• 1 <= p.length <= 20

• s contains only lowercase English letters.

• p contains only lowercase English letters, '.', and '*'.

• It is guaranteed for each appearance of the character '*', there will be a previous valid character to match.

Solution 1 — Recursive Match with Conditions

This uses recursion to match the string and pattern step by step. It checks if the current characters match and handles how * behaves in the pattern. This one follows the problem description closely, and it's helpful for understanding how each piece of the pattern applies.

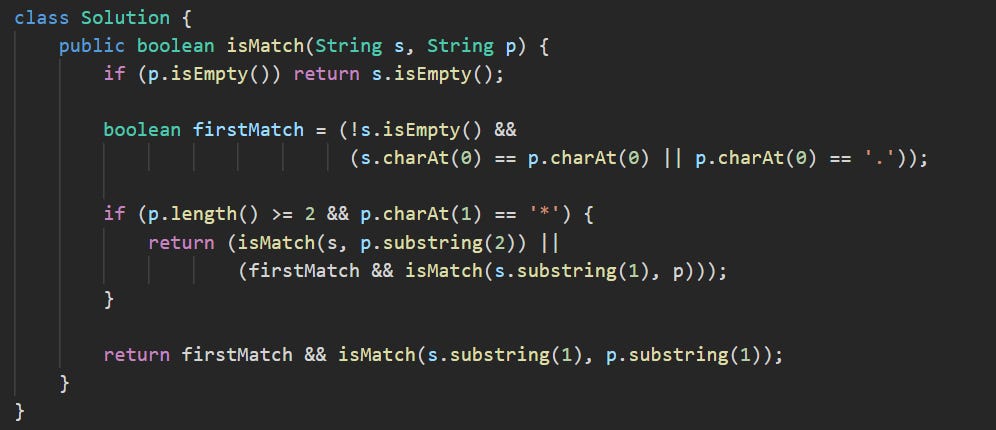
class Solution {
    public boolean isMatch(String s, String p) {

We define the method. It takes two strings, one for the input and one for the pattern, and returns a boolean indicating whether the pattern fully matches the input.

if (p.isEmpty()) return s.isEmpty();

If the pattern is empty, then for a match to happen, the string must also be empty. If it’s not, the match fails.

boolean firstMatch = (!s.isEmpty() &&
                      (s.charAt(0) == p.charAt(0) || p.charAt(0) == '.'));

We check if the first character in the string matches the first in the pattern. This is either a direct character match or a match through the dot, which allows any single character.

if (p.length() >= 2 && p.charAt(1) == '*') {
    return (isMatch(s, p.substring(2)) ||
            (firstMatch && isMatch(s.substring(1), p)));
}

If the next character in the pattern is *, we’ve got two paths to check. The first skips over the pair of characters, treating * as matching zero of the previous character. The second path consumes one character from the string while the pattern pointer stays put, letting the '*' stand for one or more repeats of the preceding element.. That way, we use the * to repeat the previous pattern character if it matches.

return firstMatch && isMatch(s.substring(1), p.substring(1));
    }
}

If there’s no *, then we only move forward if the first characters matched. We trim both strings by one and continue.

This solution is helpful for understanding how pattern matching works, especially when handling a *. The logic sticks closely to how the rules are described, but the recursive calls end up rechecking the same parts of the string and pattern over and over. It works well for short inputs, but performance drops quickly with longer ones. The worst-case time cost is about O(2^{m+n}) because every '*' can branch the recursion in two directions, while the call stack still needs only O(m + n) space.

Solution 2 — Dynamic Programming with a 2D Table

The recursive solution ends up rechecking the same substring combinations many times. This one avoids that by storing the results in a table, so we only compute each possible string-pattern pair once. Every cell in the table tells us whether a portion of the input matches a portion of the pattern. After we fill it in, there's no repeated work.

class Solution {
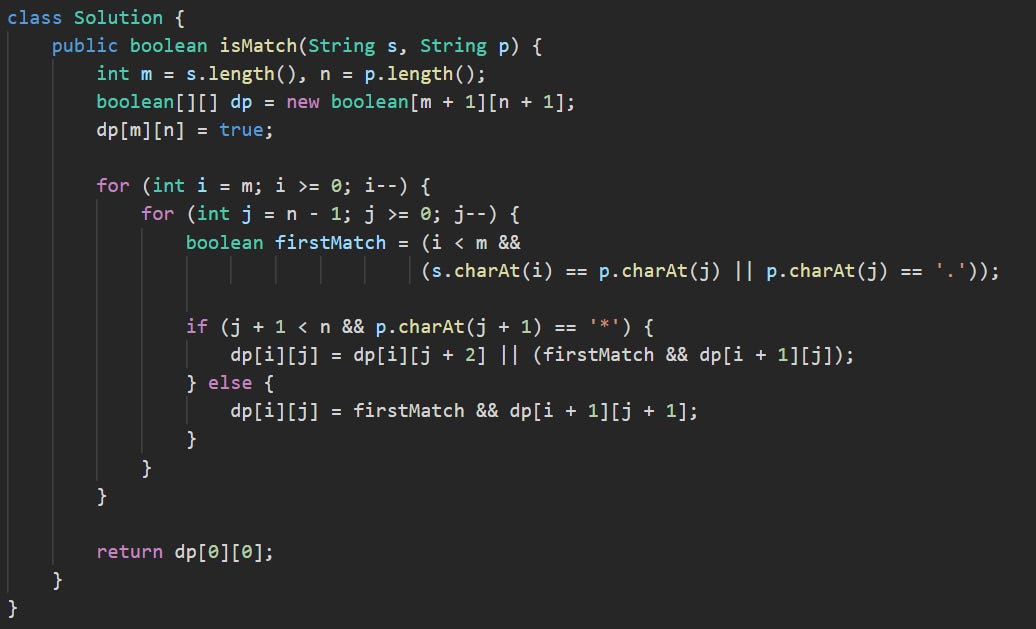
    public boolean isMatch(String s, String p) {

We define the same method, but this time we’ll use a 2D array to track matching results.

int m = s.length(), n = p.length();
boolean[][] dp = new boolean[m + 1][n + 1];
dp[m][n] = true;

The table has one extra row and column to represent the empty string. dp[m][n] = true means an empty string matches an empty pattern.

for (int i = m; i >= 0; i--) {
    for (int j = n - 1; j >= 0; j--) {
        boolean firstMatch = (i < m &&
                             (s.charAt(i) == p.charAt(j) || p.charAt(j) == '.'));

We fill the table bottom-up (from the end of both strings toward the start). At each position, we check if the current characters match. The dot matches anything, just like before.

        if (j + 1 < n && p.charAt(j + 1) == '*') {
            dp[i][j] = dp[i][j + 2] || (firstMatch && dp[i + 1][j]);
        } else {
            dp[i][j] = firstMatch && dp[i + 1][j + 1];
        }
    }
}

If the next character in the pattern is *, we can skip it along with its preceding character or we can use it to match more characters in the string if the current ones match. If there’s no *, then we only move forward when the current characters match.

return dp[0][0];
    }
}

After the loop, the answer is stored at the top-left of the table. If that cell is true, the entire string matches the pattern.

This version avoids the repeated work by keeping track of results in a table. It handles all the pattern logic in a clean way and scales much better for longer inputs. Once the table is filled in, the match result is already set and doesn't require any backtracking. The time complexity is O(m × n), and space complexity is also O(m × n), where m and n are the lengths of the input string and the pattern.

Recursive Match with Conditions — Copy and Paste

class Solution {
    public boolean isMatch(String s, String p) {
        if (p.isEmpty()) return s.isEmpty();

        boolean firstMatch = (!s.isEmpty() &&
                              (s.charAt(0) == p.charAt(0) || p.charAt(0) == '.'));

        if (p.length() >= 2 && p.charAt(1) == '*') {
            return (isMatch(s, p.substring(2)) ||
                    (firstMatch && isMatch(s.substring(1), p)));
        }

        return firstMatch && isMatch(s.substring(1), p.substring(1));
    }
}

Dynamic Programming with a 2D Table — Copy and Paste

class Solution {
    public boolean isMatch(String s, String p) {
        int m = s.length(), n = p.length();
        boolean[][] dp = new boolean[m + 1][n + 1];
        dp[m][n] = true;

        for (int i = m; i >= 0; i--) {
            for (int j = n - 1; j >= 0; j--) {
                boolean firstMatch = (i < m &&
                                     (s.charAt(i) == p.charAt(j) || p.charAt(j) == '.'));

                if (j + 1 < n && p.charAt(j + 1) == '*') {
                    dp[i][j] = dp[i][j + 2] || (firstMatch && dp[i + 1][j]);
                } else {
                    dp[i][j] = firstMatch && dp[i + 1][j + 1];
                }
            }
        }

        return dp[0][0];
    }
}