This problem asks you to find the most water that can be trapped between two vertical lines on a chart. Each line is defined by an array of heights, where the index represents its position on the x-axis. The container is formed by choosing any two lines, and the amount of water it can hold depends on the shorter line and the distance between them.
We’ll start with a basic version that checks every pair of lines to build a clear understanding of how area is calculated. After that, we’ll walk through a more efficient method that uses two pointers to avoid redundant comparisons. Both solutions are explained in full, and copy-ready Java code at the very end.
You are given an integer array height of length n. There are n vertical lines drawn such that the two endpoints of the i-th line are (i, 0) and (i, height[i]).
Find two lines that together with the x-axis form a container, such that the container contains the most water.
Return the maximum amount of water a container can store.
Notice that you may not slant the container.
Example 1:
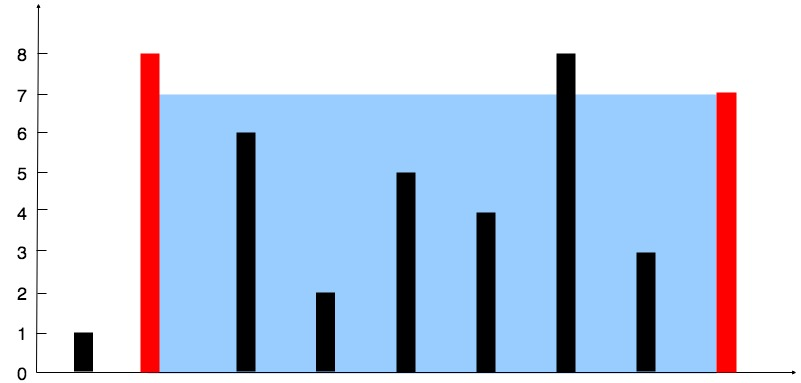
Input: height = [1,8,6,2,5,4,8,3,7]
Output: 49
Explanation: The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.
Example 2:
Input: height = [1,1]
Output: 1
Constraints:
n == height.length
2 <= n <= 10⁵
0 <= height[i] <= 10⁴
Solution 1: Brute Force (Will Time Out on Submit)
This tries every pair of lines to find the container with the most water. It walks through all possible combinations using two loops and tracks the largest area seen. It works on smaller arrays, but the number of comparisons grows too fast for larger inputs. LeetCode will reject it for taking too long.
class Solution {
public int maxArea(int[] height) {
We define a public method named maxArea. It takes an array of integers, where each element represents the height of a vertical line at that index. The goal is to find the largest rectangular area between any two of these lines.
int max = 0;
This variable keeps track of the largest area we’ve seen so far. It starts at zero and gets updated whenever we find a better candidate.
for (int i = 0; i < height.length; i++) {
for (int j = i + 1; j < height.length; j++) {
These two loops go through every possible pair of lines. The outer loop picks the first line. The inner loop tests every second line that comes after it, making sure each pair is only tested once.
int width = j - i;
int minHeight = Math.min(height[i], height[j]);
int area = width * minHeight;
max = Math.max(max, area);
We compute the width by taking the distance between the two indices. Since water can't go higher than the shorter line, we take the minimum of the two heights. Multiplying the width by the height gives us the container’s area. If this area is larger than the current best, we update the max.
}
}
return max;
}
}
After all pairs have been checked, we return the largest area found.
Even though this method is valid and gives the right result, it runs far too slowly on large input. The reason is that both loops create every possible pair, which leads to a time cost of O(n²). That means a small increase in input size causes a huge spike in comparisons. The space cost stays at O(1) because we don’t use any extra memory. It’s still worth stepping through this version to see how width, height, and area come together, and why trying every pair isn’t practical at scale.
Solution 2: Two-Pointer Solution
This solution skips checking every pair. It starts with the widest container and works inward, always moving the shorter line. That gives a chance to find a better height while the width shrinks. The method finishes in linear time and handles large arrays easily.
class Solution {
public int maxArea(int[] height) {
We define the same method again, but now with a faster strategy. Instead of checking all pairs, we begin with the widest pair and narrow things down by always choosing the better move based on height.
int max = 0;
int left = 0;
int right = height.length - 1;
We set two pointers: one at the start and one at the end. The idea is that the widest container comes from the outermost lines. From there, we’ll try to improve the height while width gets smaller.
while (left < right) {
We keep going as long as the pointers haven’t crossed. Once they meet, we’ve tried all viable combinations.
int width = right - left;
int minHeight = Math.min(height[left], height[right]);
int area = width * minHeight;
max = Math.max(max, area);
We measure the area between the two pointers just like before. Width is the difference in position. Height is based on the shorter of the two lines. We compute the area and update max if it’s larger.
We move the pointer that’s on the shorter line. Moving the taller line wouldn't help because the shorter one is already limiting the height. Shifting the shorter pointer might lead to a taller replacement, giving a chance at a bigger area.
}
return max;
}
}
When the loop finishes, we’ve found the largest area and return it.
This version works because it avoids checking combinations that can’t possibly improve the result. By moving only the pointer at the shorter line, it focuses on situations where height might improve while keeping the search efficient. Every line gets visited at most once, so the time cost stays at O(n), which scales well even with the largest inputs. The space cost is O(1) because no extra memory is used outside the input and a few variables. This method is fast, simple to write, and gets accepted on LeetCode without any time issues.
Solution 1: Brute Force (Will Time Out on Submit) — Copy and Paste
class Solution {
public int maxArea(int[] height) {
int max = 0;
for (int i = 0; i < height.length; i++) {
for (int j = i + 1; j < height.length; j++) {
int width = j - i;
int minHeight = Math.min(height[i], height[j]);
int area = width * minHeight;
max = Math.max(max, area);
}
}
return max;
}
}
Solution 2: Two-Pointer Solution — Copy and Paste
class Solution {
public int maxArea(int[] height) {
int max = 0;
int left = 0;
int right = height.length - 1;
while (left < right) {
int width = right - left;
int minHeight = Math.min(height[left], height[right]);
int area = width * minHeight;
max = Math.max(max, area);
if (height[left] < height[right]) {
left++;
} else {
right--;
}
}
return max;
}
}
