You’re given a number between 1 and 3999 and need to turn it into Roman numerals. The rules behind the numeral system are fixed, with symbols like I for 1, V for 5, and X for 10. Some numbers are written by stacking symbols together, while others use subtraction pairs like IV for 4 or CM for 900. You don’t need to validate the input, just return the Roman string that matches it.
The first solution walks through the values from largest to smallest and subtracts as it goes. It's simple, works well, and helps make the system easier to follow. The second solution uses indexing and pre-built strings to skip the loops and get straight to the result. Both run in constant time and space, and both are included with full Java code below.
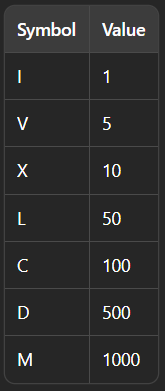
Seven different symbols represent Roman numerals with the following values:
Roman numerals are formed by appending the conversions of decimal place values from highest to lowest. Converting a decimal place value into a Roman numeral has the following rules:
If the value does not start with 4 or 9, select the symbol of the maximal value that can be subtracted from the input, append that symbol to the result, subtract its value, and convert the remainder to a Roman numeral.
If the value starts with 4 or 9 use the subtractive form representing one symbol subtracted from the following symbol, for example, 4 is 1 (I) less than 5 (V): IV and 9 is 1 (I) less than 10 (X): IX. Only the following subtractive forms are used: 4 (IV), 9 (IX), 40 (XL), 90 (XC), 400 (CD) and 900 (CM).
Only powers of 10 (I, X, C, M) can be appended consecutively at most 3 times to represent multiples of 10. You cannot append 5 (V), 50 (L), or 500 (D) multiple times. If you need to append a symbol 4 times use the subtractive form.
Given an integer, convert it to a Roman numeral.
Example 1:
Input: num = 3749
Output: "MMMDCCXLIX"
Explanation:
3000 = MMM as 1000 (M) + 1000 (M) + 1000 (M)
700 = DCC as 500 (D) + 100 (C) + 100 (C)
40 = XL as 10 (X) less of 50 (L)
9 = IX as 1 (I) less of 10 (X)
Note: 49 is not 1 (I) less of 50 (L) because the conversion is based on decimal places
Example 2:
Input: num = 58
Output: "LVIII"
Explanation:
50 = L
8 = VIII
Example 3:
Input: num = 1994
Output: "MCMXCIV"
Explanation:
1000 = M
900 = CM
90 = XC
4 = IV
Constraints:
1 <= num <= 3999
Solution 1: Greedy Subtraction
This solution goes through a list of values and keeps subtracting the biggest one that still fits. Every time we subtract, we also add the matching Roman numeral to the result. It’s direct, easy to follow, and gets the job done without much setup. The pattern of working from largest to smallest makes it a good starting point for learning how the numeral system works.
This method walks through each Roman numeral value in order from largest to smallest and subtracts it from the input number while adding the matching symbol to the result string.
class Solution {
public String intToRoman(int num) {
We define a method called intToRoman that takes in an integer from 1 to 3999 and returns its Roman numeral equivalent as a string. This part comes from the starter code provided by LeetCode.
This array holds the standard Roman numeral values, ordered from largest to smallest. That order matters because we always want to subtract the biggest number that still fits into what’s left of num. That’s what makes the greedy pattern work here. It also includes the subtractive cases like 900 or 4 so we can match things like CM and IV directly without needing special logic for them.
Each value has a Roman numeral version, and this array gives us the matching symbols in the same order as the values array. That way, index i in both arrays always refers to the same thing.
StringBuilder result = new StringBuilder();
We use a StringBuilder instead of a regular string so we can add characters to it more efficiently while we’re building the final result.
for (int i = 0; i < values.length; i++) {
We loop through every value in the list, starting from the biggest. We are going to keep working our way down until we've handled the full number.
while (num >= values[i]) {
If the current Roman numeral value is smaller than or equal to the number we still have left, we subtract it and add the symbol to our result. This loop keeps running until that’s no longer true.
num -= values[i];
We subtract the value at index i from num. This reduces the number by the amount we’ve just accounted for with a Roman numeral.
result.append(symbols[i]);
And here we add the Roman symbol for that value to the result string.
}
}
After we’ve added as many of that value as we can, we move to the next one and repeat the process.
return result.toString();
}
}
When all the values have been processed and num has reached zero, we return the full Roman numeral string that was built along the way.
This solution works well because it breaks the number down in chunks, always using the largest possible piece at every step. It handles edge cases like 4 or 900 just by including the correct symbol and value pair. The size of the values array never changes and the input number is always capped at 3999, so this whole process runs in constant time. There are no data structures that grow with the input either. The only memory used is for the fixed-size arrays and the result string that’s being built. So the time complexity is O(k) with k ≤ 15, which is effectively O(1) for all valid inputs in the 1–3999 range. The space complexity is also O(1), because no part of the logic grows with the input.
Solution 2: Index-Based Fast Mapping (Better for Interviews)
Instead of subtracting values one by one, this method builds the result by breaking the number into digits and using those digits to grab the matching Roman strings. Each place value has its own set of options, and we just stitch the right pieces together. It’s fast, precise, and shows a strong grasp of structure and reuse, which often goes over well in interviews.
This version takes the number apart by digit, one place at a time, and uses that digit as an index into arrays of Roman numeral strings. Each part is then glued together into the final result.
class Solution {
public String intToRoman(int num) {
We define the same method again, but the way it works is different. We won’t be subtracting anything. Instead, we’ll use digit positions to look up the right Roman symbols.
String[] thousands = {"", "M", "MM", "MMM"};
This array gives us all the valid Roman numeral values for the thousands digit. The index tells us how many thousands to write. So if the number starts with 2000, we’ll use MM.
Here we’ve got all possible Roman representations of the hundreds place. This covers everything from 0 up to 900. Strings like CD and CM take care of the subtractive cases without any extra code.
We get each digit by dividing or taking the remainder. num / 1000 gives us the thousands digit, which tells us which string to use from the thousands array. The same goes for the hundreds, tens, and ones. We just build the result by stringing them all together in order.
This works well because the input is always in a fixed range from 1 to 3999. We’re not looping, subtracting, or checking anything conditionally. Everything is driven by array indexing and simple math. Each digit is used to pull a value directly from a pre-filled list, and we build the final result by gluing four small pieces together. There’s no extra computation, no duplication, and no temporary logic to track. That keeps things predictable and easy to follow. The time complexity is O(1), and the space stays O(1) too, because nothing in this solution scales with the size of the input, same as the first solution.
What makes this version stand out in interviews, even with the same complexity as the first, is how clearly it separates structure from logic. It doesn’t repeat symbols in a loop or rely on subtracting one value at a time. Instead, it shows that you can think in terms of patterns, precompute reusable pieces, and avoid extra work altogether. It gives the same result but with less motion and more clarity, which tends to leave a better impression when you're asked to walk someone through your thinking.
Solution 1: Greedy Subtraction — Copy and Paste
class Solution {
public String intToRoman(int num) {
int[] values = {1000, 900, 500, 400, 100, 90,
50, 40, 10, 9, 5, 4, 1};
String[] symbols = {"M", "CM", "D", "CD", "C", "XC",
"L", "XL", "X", "IX", "V", "IV", "I"};
StringBuilder result = new StringBuilder();
for (int i = 0; i < values.length; i++) {
while (num >= values[i]) {
num -= values[i];
result.append(symbols[i]);
}
}
return result.toString();
}
}
Solution 2: Index-Based Fast Mapping — Copy and Paste
