Roman numerals follow a fixed set of rules built around a small group of letters. Each one stands for a number, and the way you combine them depends on both size and position. You add when smaller values come after larger ones and subtract when they come before. So VI is 6, but IV is 4. The system doesn’t change, and the input is always valid, so all you need to do is turn the string into the number it represents.
The first solution moves through the string from left to right and compares each symbol to the one that follows it. If the next one is larger, it subtracts the current value. Otherwise, it adds it. The second version works backward and skips the map entirely by using a fixed array for fast lookup. Both versions go through the string one time, stay consistent on memory use, and give the same result, just with different structure and flow.
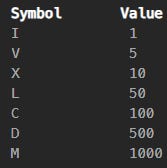
Roman numerals are represented by seven different symbols: I, V, X, L, C, D and M.
For example, 2 is written as II in Roman numeral, just two ones added together. 12 is written as XII, which is simply X + II. The number 27 is written as XXVII, which is XX + V + II.
Roman numerals are usually written largest to smallest from left to right. However, the numeral for four is not IIII. Instead, the number four is written as IV. Because the one is before the five we subtract it making four. The same principle applies to the number nine, which is written as IX. There are six instances where subtraction is used:
I can be placed before V (5) and X (10) to make 4 and 9.
X can be placed before L (50) and C (100) to make 40 and 90.
C can be placed before D (500) and M (1000) to make 400 and 900.
Given a roman numeral, convert it to an integer.
Example 1:
Input: s = "III"
Output: 3
Explanation: III = 3.
Example 2:
Input: s = "LVIII"
Output: 58
Explanation: L = 50, V= 5, III = 3.
Example 3:
Input: s = "MCMXCIV"
Output: 1994
Explanation: M = 1000, CM = 900, XC = 90 and IV = 4.
Constraints:
1 <= s.length <= 15
s contains only the characters ('I', 'V', 'X', 'L', 'C', 'D', 'M').
It is guaranteed that s is a valid roman numeral in the range [1, 3999].
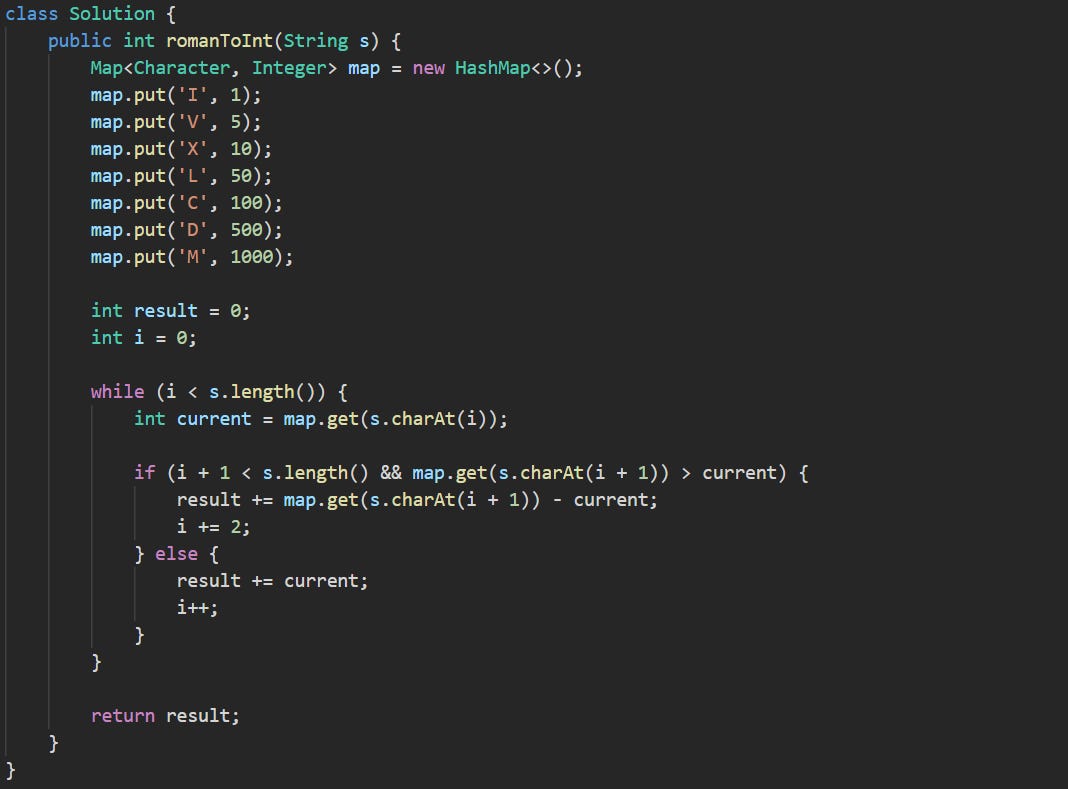
Solution 1: Left-to-Right Subtractive Check
This solution works by going through the Roman numeral string from left to right, one symbol at a time. The main idea is that if a smaller value comes before a larger one, you subtract it instead of adding it. That reflects how Roman numerals handle numbers like 4 (IV) or 90 (XC). Everything else is just added to the total as we move forward.
This method doesn’t need to memorize pairs or build temporary strings. Instead, it uses a map to turn each character into a number, then checks each number in the order it appears to decide whether it should be added or subtracted.
class Solution {
public int romanToInt(String s) {
We start by defining a method called romanToInt that takes a Roman numeral as a string and gives us back the integer version. This is the same method signature that LeetCode gives you to start with.
This map connects each Roman symbol to its value. That’s all we need to understand the input. The values follow fixed rules, so this map stays the same for every input and doesn’t change. Because we put them in a HashMap, we can look up values for each character without writing a long series of if-statements.
int result = 0;
int i = 0;
We’ll use result to build up the final value as we process the string. The variable i helps us track where we are in the input.
while (i < s.length()) {
int current = map.get(s.charAt(i));
Here we start looping through the input from the beginning. We grab the numeric value of the current Roman character by looking it up in our map. That gives us something we can compare.
if (i + 1 < s.length() && map.get(s.charAt(i + 1)) > current) {
result += map.get(s.charAt(i + 1)) - current;
i += 2;
This is the part where the Roman numeral logic shows up. If the number that comes after the current one is larger, that means this is a subtractive case. So instead of adding both numbers, we take the next one and subtract the current one from it. That’s what the system does with things like IV or CM. Once that pair has been processed, we skip ahead by two positions.
} else {
result += current;
i++;
}
}
If we’re not in one of those subtractive cases, then we just add the current value to the result. Then we move ahead one position and repeat.
return result;
}
}
After we’ve gone through the full string, the total is ready to return.
This is simple and dependable way of solving the problem. Each character is handled in place, and the map gives us fast access to values. By comparing one character to the next, we automatically cover all the rules of Roman numerals without any extra code for each special case. The loop runs through the input string once, and the map is fixed in size no matter what the input looks like. So the time complexity is O(n), where n is the number of characters in the string. The space usage stays O(1) because we only use the map and a few small variables. This version matches how Roman numerals are read and lets the system’s structure do the work for us.
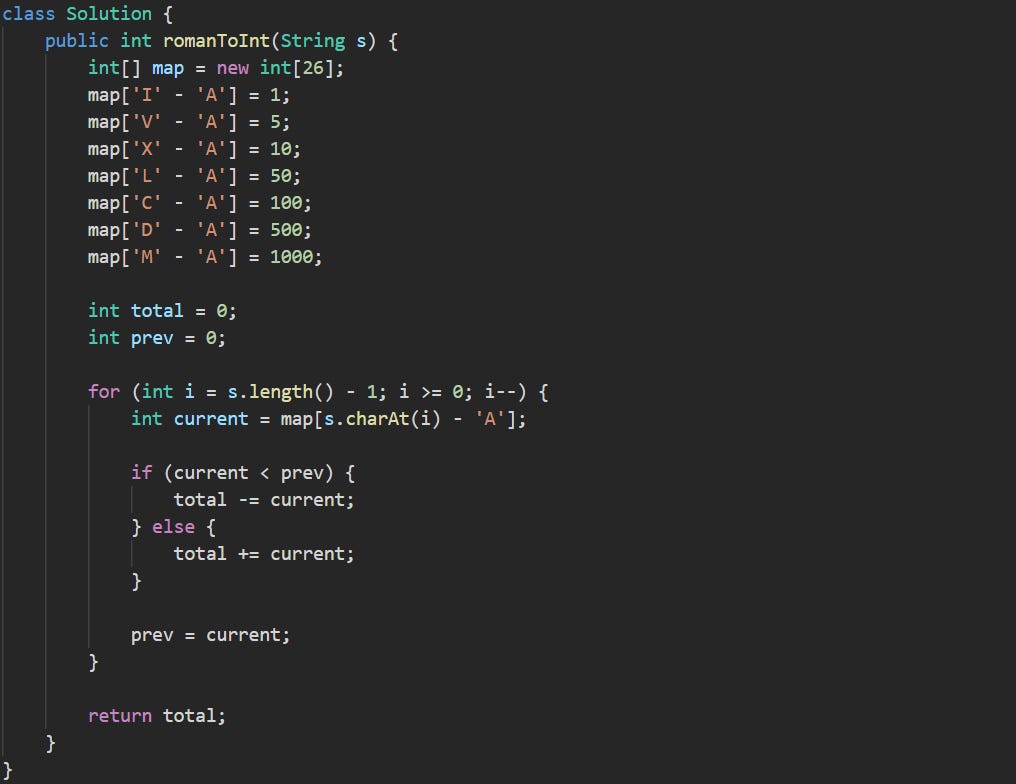
Solution 2: Backward Scan with Indexed Lookup
This solution reads the input in reverse. We start from the end of the string and work our way back to the beginning, which changes how the subtraction logic is applied. In Roman numerals, smaller values that come before larger ones should be subtracted, so by going from right to left, we can compare each character to the one we just processed. That removes the need for lookahead and lets us avoid checking character pairs.
The Roman numeral system always builds numbers from the largest values down, but it uses subtraction in a few special cases. By scanning from the end, we make that easier to detect with a single comparison.
class Solution {
public int romanToInt(String s) {
We start again with the same method signature. This version will use the same logic as the Roman numeral system but scan the string in reverse.
Instead of a HashMap, we use a simple array with 26 slots, one for each uppercase letter. Each Roman symbol gets placed at the index that matches its alphabetical position, which is just its character minus 'A'. This lets us grab values quickly without hashing or checking keys. Every lookup takes the same amount of time, and the array size stays fixed.
int total = 0;
int prev = 0;
We set up two integers. One tracks the result, and the other remembers the last value we processed. This is what we’ll compare against to decide if we should subtract or add the current symbol.
for (int i = s.length() - 1; i >= 0; i--) {
int current = map[s.charAt(i) - 'A'];
Now we walk through the string backwards. We take the current character, turn it into its index in the alphabet, and use that to grab the corresponding value from our array. That’s our current value.
if (current < prev) {
total -= current;
} else {
total += current;
}
If the current value is smaller than the last one we saw, that means it came before a larger one and should be subtracted. Otherwise we add it. That’s how Roman subtraction works. It only applies when a smaller value comes before a larger one.
prev = current;
}
After processing each character, we update prev so we can compare it to the next one in the loop.
return total;
}
}
When we’ve gone through the string from end to beginning, we return the final total.
This version cuts out map lookups and extra checks by shifting the direction we process the string. Instead of needing to look ahead or pair characters, it just compares the current symbol with what came before. That matches how the rules work without needing to handle each subtraction case one by one. The array is fixed in size and only holds 26 values, which covers the entire uppercase alphabet. The loop goes through the string once, and the amount of work stays constant for each character. Time complexity is O(n), and the space usage stays O(1).
Solution 1: Left-to-Right Subtractive Check — Copy and Paste
class Solution {
public int romanToInt(String s) {
Map<Character, Integer> map = new HashMap<>();
map.put('I', 1);
map.put('V', 5);
map.put('X', 10);
map.put('L', 50);
map.put('C', 100);
map.put('D', 500);
map.put('M', 1000);
int result = 0;
int i = 0;
while (i < s.length()) {
int current = map.get(s.charAt(i));
if (i + 1 < s.length() && map.get(s.charAt(i + 1)) > current) {
result += map.get(s.charAt(i + 1)) - current;
i += 2;
} else {
result += current;
i++;
}
}
return result;
}
}
Solution 2: Backward Scan with Indexed Lookup — Copy and Paste
class Solution {
public int romanToInt(String s) {
int[] map = new int[26];
map['I' - 'A'] = 1;
map['V' - 'A'] = 5;
map['X' - 'A'] = 10;
map['L' - 'A'] = 50;
map['C' - 'A'] = 100;
map['D' - 'A'] = 500;
map['M' - 'A'] = 1000;
int total = 0;
int prev = 0;
for (int i = s.length() - 1; i >= 0; i--) {
int current = map[s.charAt(i) - 'A'];
if (current < prev) {
total -= current;
} else {
total += current;
}
prev = current;
}
return total;
}
}
