LeetCode #14: Longest Common Prefix — Solved in Java
Character-by-Character Matching and Sort and Compare First and Last
Prefixes are shared starting fragments of words, and the problem here is to find the longest one that shows up at the beginning of every string in a list. That prefix has to start from the first character and continue as far as all the strings agree. It doesn’t matter how long the rest of each word is, just how much they have in common at the front.
In the first solution, we check every character one by one across all the strings and stops the moment anything disagrees. It moves carefully and directly through the characters without changing the input. The second sorts the array, which naturally places the biggest differences at opposite ends, then compares just the first and last strings to find the answer. Both return the same result, but the way they reach it is completely different.
LeetCode: Longest Common Prefix
Write a function to find the longest common prefix string amongst an array of strings.
If there is no common prefix, return an empty string
"".Example 1:
Input: strs = ["flower","flow","flight"] Output: "fl"Example 2:
Input: strs = ["dog","racecar","car"] Output: "" Explanation: There is no common prefix among the input strings.Constraints:
1 <= strs.length <= 200
0 <= strs[i].length <= 200
strs[i]consists of only lowercase English letters if it is non-empty.
Solution 1: Character-by-Character Matching
This method starts with the first string and works through it one character at a time, comparing each position against all the other strings. If they all match at that position, we move forward. The moment one of them doesn't, we stop and return the part that worked. This kind of check stays readable and gets to the point without extra setup or memory use.
This version doesn’t try to optimize the structure of the input or rearrange anything. It just walks through every character step by step, checking directly what’s in front of it. Nothing is preprocessed or stored aside from a few variables, which keeps it easy to trace through.
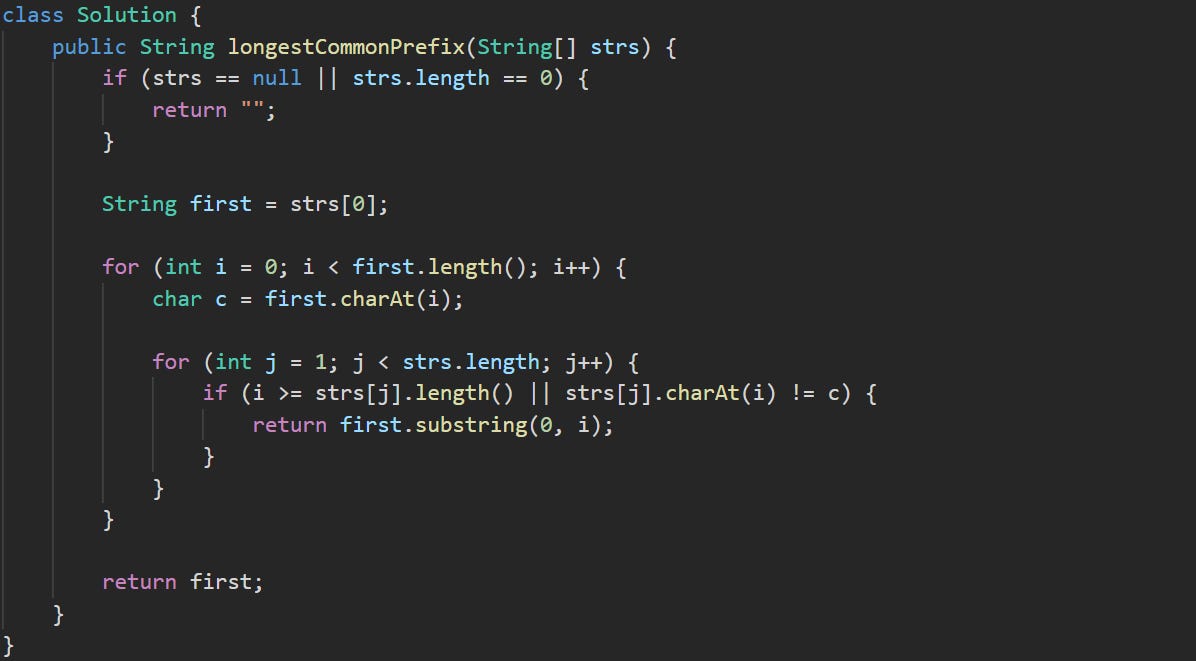
class Solution {
public String longestCommonPrefix(String[] strs) {We define a method called longestCommonPrefix that takes an array of strings and returns a string. This is the method signature provided by LeetCode.
if (strs == null || strs.length == 0) {
return "";
}Before we do any comparisons, we check that the input is actually usable. If the array is missing or it has no content, there’s no point continuing. Returning an empty string avoids unnecessary errors and gives a safe fallback.
String first = strs[0];We start by pulling the first word in the array. That becomes the reference point for every character comparison. If all the strings are going to share a prefix, then it has to start here.
for (int i = 0; i < first.length(); i++) {
char c = first.charAt(i);This loop walks through the characters of the first word. We’re only interested in checking each position across all strings one by one. If the others agree with the current character c, we keep going. If not, we stop there.
for (int j = 1; j < strs.length; j++) {
if (i >= strs[j].length() || strs[j].charAt(i) != c) {
return first.substring(0, i);
}
}Here’s where the actual comparison happens. For each character in the first word, we look at the same spot in every other string. If any string runs out of characters or has a different one at that position, then that marks the end of the shared part. The condition also guards against index errors in case one word is shorter than the first.
If all strings pass the test for that character, the loop continues to the next one. If not, we stop and return a slice of the first word up to the point where everything still matched.
return first;If the loop finishes without finding any disagreement, it means all the strings matched completely with the first one. We return it in full, since no string had a reason to break the match early.
Mechanically, this solution loops over every character in the first word and compares it to the character at the same index in every other string. It stops early as soon as one string is too short or disagrees at that position. Time complexity is O(n * m), where n is the number of strings and m is the length of the shortest one. Space complexity is O(1) because no extra memory is used outside the loop counters and character references.
Solution 2: Sort and Compare First and Last
Instead of comparing every string to the first one, this version sorts the array first. Sorting puts strings with common prefixes closer together. That means the first and last strings in the sorted array show the widest possible difference, so we only need to compare those two. The overlap at the start of those two strings is guaranteed to be the full shared prefix.
Rather than stepping through each string individually, this method takes advantage of what sorting does to the structure. After sorting, the answer is already baked into just the first and last strings, and only those two need to be checked character by character.
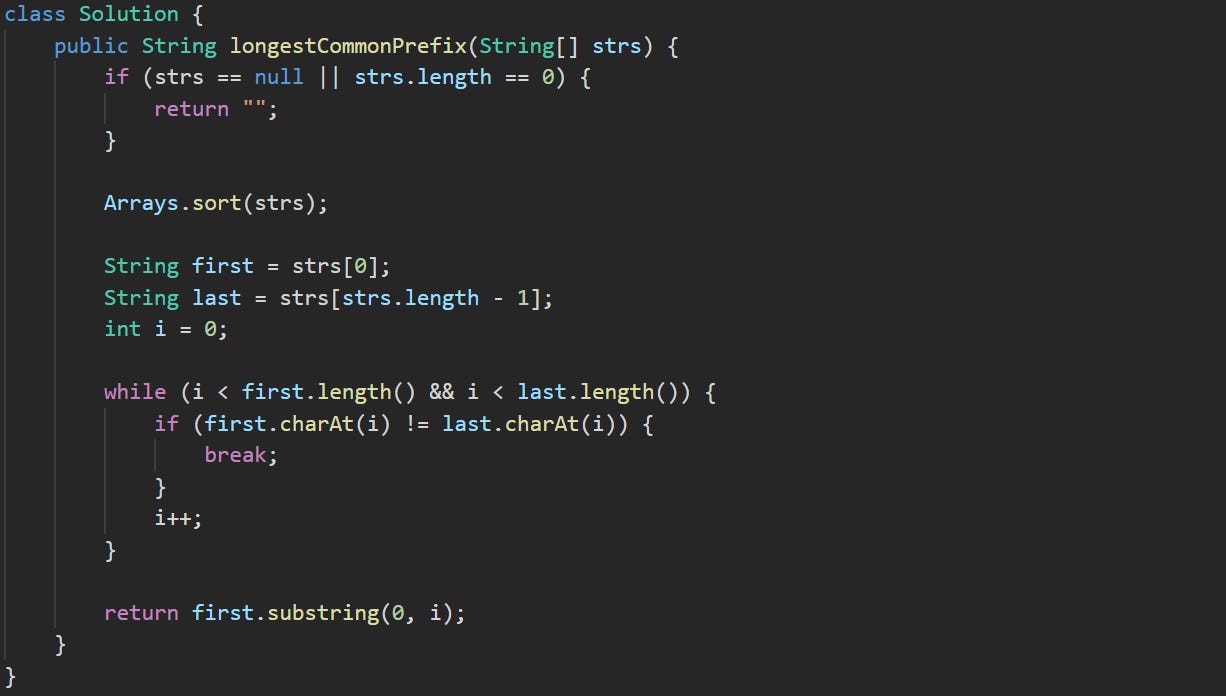
public String longestCommonPrefix(String[] strs)We define the same method again. It takes an array of strings and returns the prefix that every string in the array has in common at the start, again this is the default provided by LeetCode.
if (strs == null || strs.length == 0) {
return "";
}Same as before, we check for a missing or empty array. If there’s nothing to work with, we return an empty string.
Arrays.sort(strs);Here’s where the change starts. By sorting the array, we arrange the words alphabetically. That puts the ones that are most alike close together. The string at the front of the list and the one at the end now represent the furthest difference between any two items in the array. So if we compare those two and find what they share at the start, we know it covers every string in between too.
String first = strs[0];
String last = strs[strs.length - 1];
int i = 0;We store the first and last strings after the sort, and we set up a counter i to track how far the two match.
while (i < first.length() && i < last.length()) {
if (first.charAt(i) != last.charAt(i)) {
break;
}
i++;
}We loop through both strings from the beginning. At each position, we compare the characters. If they match, we move to the next one. If we hit a spot where the characters are different, that’s the limit of the shared prefix. We stop there.
This works because every string between the first and last is bound to share at least that much overlap, otherwise the first and last wouldn’t have matched that far after the sort.
return first.substring(0, i);When the loop ends, we return the part of the first word that matched. That slice from the start up to i holds the answer.
This solution sorts the array, then walks character by character through only the first and last strings. The idea is that if they agree up to a certain point, everything between them in the sorted list will also share that same prefix. Sorting takes O(n log n × k) time, where n is the number of strings and k is their average length, because each comparison can scan up to k characters. The final prefix scan over the first and last strings adds O(m) time, where m is the length of the shortest string. Space stays O(1) apart from the temporary O(n) buffer that Java’s TimSort allocates.
Solution 1: Character-by-Character Matching — Copy and Paste
class Solution {
public String longestCommonPrefix(String[] strs) {
if (strs == null || strs.length == 0) {
return "";
}
String first = strs[0];
for (int i = 0; i < first.length(); i++) {
char c = first.charAt(i);
for (int j = 1; j < strs.length; j++) {
if (i >= strs[j].length() || strs[j].charAt(i) != c) {
return first.substring(0, i);
}
}
}
return first;
}
}Solution 2: Sort and Compare First and Last — Copy and Paste
class Solution {
public String longestCommonPrefix(String[] strs) {
if (strs == null || strs.length == 0) {
return "";
}
Arrays.sort(strs);
String first = strs[0];
String last = strs[strs.length - 1];
int i = 0;
while (i < first.length() && i < last.length()) {
if (first.charAt(i) != last.charAt(i)) {
break;
}
i++;
}
return first.substring(0, i);
}
}