LeetCode #15: 3Sum — Solved in Java

Hash Set and Unsorted Triplets and Sorted Scan with Two Pointers

Image Source

Finding three numbers that add up to zero sounds like a basic task, but the challenge is in handling duplicates and covering every combination without wasting time. The triplets can come from anywhere in the list, and they don’t have to be in order. What matters is that each group adds up exactly right and doesn’t show up more than once.

Today, we will go over a solution that loops through each number and another that looks for matching pairs with a hash set, building triplets as it goes. The second sorts the input first and then uses two pointers to scan from both sides, skipping over repeated values while it narrows in on the result. Both reach the same groups, but the way they scan, match, and avoid duplicates couldn’t be more different.

LeetCode: 3Sum

Given an integer array nums, return all the triplets [nums[i], nums[j], nums[k]] such that i != j, i != k, and j != k, and nums[i] + nums[j] + nums[k] == 0.

Notice that the solution set must not contain duplicate triplets.

Example 1:

Input: nums = [-1,0,1,2,-1,-4]
Output: [[-1,-1,2],[-1,0,1]]
Explanation: 
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0.
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0.
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0.
The distinct triplets are [-1,0,1] and [-1,-1,2].
Notice that the order of the output and the order of the triplets does not matter.

Example 2:

Input: nums = [0,1,1]
Output: []
Explanation: The only possible triplet does not sum up to 0.

Example 3:

Input: nums = [0,0,0]
Output: [[0,0,0]]
Explanation: The only possible triplet sums up to 0.

Constraints:

• 3 <= nums.length <= 3000

• -105 <= nums[i] <= 105

Solution 1: Hash Set and Unsorted Triplets

This version loops through the array with one fixed number and checks if a matching pair completes the sum to zero. A hash set tracks the values we've already seen, and each valid triplet is sorted before it’s added so duplicates don’t slip through.

It uses the same outer structure as a full brute-force scan but skips the third loop by checking for the needed number directly with a set.

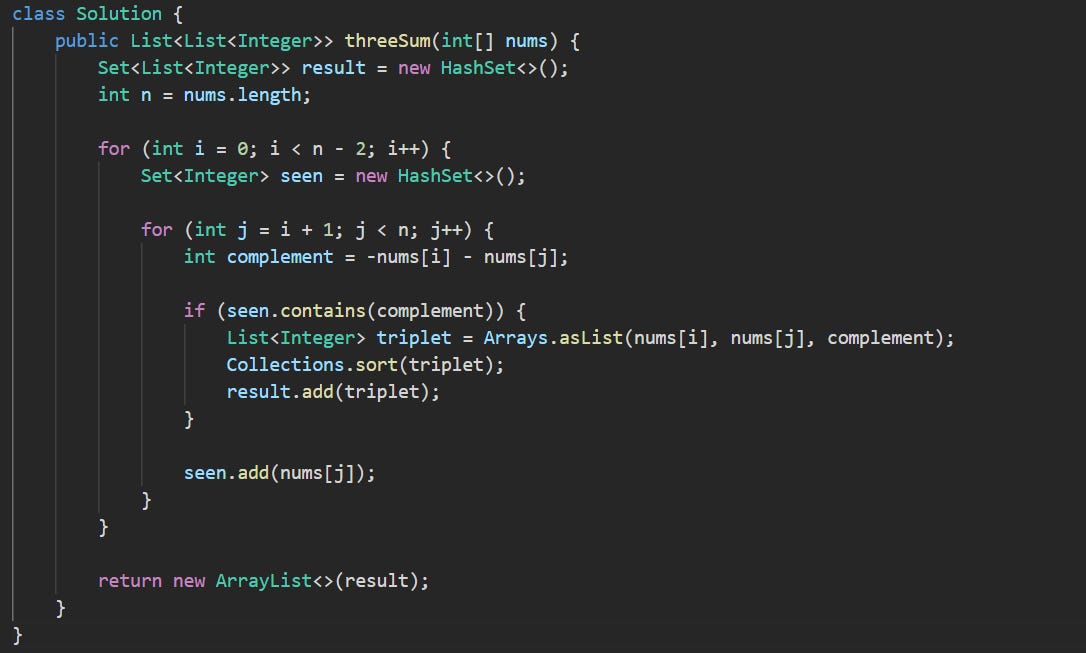
public List<List<Integer>> threeSum(int[] nums)

The method takes an array of integers and finds every unique group of three numbers that adds up to zero. The return is a list of those groups, each one stored as a list of its own.

Set<List<Integer>> result = new HashSet<>();

A set is used here to skip duplicates without needing to manually track them. Each triplet will be sorted before going into the set, so a group like [1, -1, 0] and [-1, 1, 0] both end up as [−1, 0, 1].

int n = nums.length;

Grabbing the array size up front makes the loop cleaner and avoids repeating the length check.

for (int i = 0; i < n - 2; i++) {

We start with one anchor number at index i, which means we’re looking for two others later in the array that balance it out to zero.

Set<Integer> seen = new HashSet<>();

Every new anchor resets the seen set. It stores numbers we've looked at so far in the current loop. If a number appears that completes a sum of zero with the anchor and current value, we already know it’s valid.

for (int j = i + 1; j < n; j++) {

This inner loop checks each number to the right of the anchor, one at a time, and compares it to the rest of the values seen so far.

int complement = -nums[i] - nums[j];

This line figures out the number that’s missing to hit zero. If you think of the triplet like a + b + c = 0, then once we’ve picked a and b, the third value must be -a - b. That’s our complement. We don’t need to search for it manually because we’ll just check if it’s already in the seen set.

if (seen.contains(complement)) {

If the complement is already in the set, we’ve already passed it in the loop. That means we’ve found a triplet that sums to zero.

List<Integer> triplet = Arrays.asList(nums[i], nums[j], complement);
Collections.sort(triplet);
result.add(triplet);

We create a list out of the three values and sort them before adding to the result set. Sorting is important here because we’re relying on the set to prevent duplicates, and different value orders would otherwise slip through.

seen.add(nums[j]);

Every time we pass a number, we add it to the seen set so it’s available for future complement checks.

return new ArrayList<>(result);

Then, we return the result as a list. The set kept everything unique, so the output has no repeats and contains only valid zero-sum triplets.

This method runs with two nested loops, but avoids scanning every triple directly by offloading the third value check to a hash set. Instead of hunting through the rest of the array, it just asks “have we already seen the number that would finish this group?” That lookup step makes the process faster without changing how the values are picked. Sorting each match before storing it lets the set handle duplicates without extra bookkeeping. The full array never needs to be sorted, only the matching triplets when they’re found. Time complexity is O(n²), where n is the number of values in the input. The memory use depends on how many triplets end up in the result, plus whatever’s held in the temporary set while each anchor loops through the rest. That set can grow up to the full array length in the worst case, so total space is about the number of results plus one set that grows and resets each round.

Solution 2: Sorted Scan with Two Pointers

This solution starts by sorting the input, then uses two pointers to search for matches. Sorting helps cut out repeated work and lets the scan move based on how the current sum compares to zero.

When sorted, we don't need any extra memory or manual tracking. The pointer movement and duplicate skipping all follow from how the numbers are ordered.

public List<List<Integer>> threeSum(int[] nums)

This method also takes an array of integers and returns every valid triplet that totals zero. Each group in the result is stored as a separate list.

List<List<Integer>> result = new ArrayList<>();
Arrays.sort(nums);

The array is sorted first, which means we can rely on the order of numbers while scanning. This makes it easier to avoid repeated groups and adjust the left/right ends depending on the total sum.

for (int i = 0; i < nums.length - 2; i++) {

Each pass through this loop treats nums[i] as the fixed starting value in the triplet. We stop at length −2 since we’ll always need two more values after i.

if (i > 0 && nums[i] == nums[i - 1]) {
    continue;
}

This line skips repeated anchor values. If the current number is the same as the one right before it, we move on to avoid repeating a triplet we already checked.

int left = i + 1;
int right = nums.length - 1;

These are the two pointers that scan the remaining part of the array. left starts just after the anchor, and right starts from the end. We’ll shift them based on the current sum.

while (left < right) {
    int sum = nums[i] + nums[left] + nums[right];

Inside this loop, we try combining the anchor with the values at both pointers. If the total adds up to zero, we store the triplet. If it’s too low or too high, we move the pointers to adjust.

if (sum == 0) {

When the three numbers cancel each other out, we’ve got a match.

result.add(Arrays.asList(nums[i], nums[left], nums[right]));

We store the triplet as a list. Because the array is sorted, we don’t need to sort the triplet again.

while (left < right && nums[left] == nums[left + 1]) {
    left++;
}

while (left < right && nums[right] == nums[right - 1]) {
    right--;
}

If either pointer is sitting on repeated values, we skip past them before moving on. This helps avoid triplets with the same values showing up more than once.

left++;
right--;

We move both pointers inward after recording a valid triplet. This keeps the scan moving and avoids double counting.

} else if (sum < 0) {
    left++;
} else {
    right--;
}

If the total is too small, we move left forward to raise the sum. If it’s too big, we pull right back to lower it. Sorting makes this possible because we know moving toward larger or smaller numbers will shift the sum in the right direction.

return result;

After the loop finishes, we return the list of results. All the triplets are unique and in sorted order.

Sorting the array makes the logic cleaner and cuts out a lot of waste. Once we fix one number, the rest can be scanned in place without needing any extra structures or checks. The pointer math keeps things tight, and the skip-over logic helps avoid repeating work we've already done.

This one takes a different route by preparing the input ahead of time. After everything is sorted, you don’t need hash sets or repeated value tracking by hand. The pointer scan takes care of it as you move in from both sides. The sorting step opens the door to skip duplicates as they come and decide how to move left and right based on how far off the sum is. Compared to the first solution, which reacts as values are found, this one narrows things down before checking anything. Both reach the same goal, but this version trims extra work early and avoids the overhead of sorting each triplet. Time complexity is still O(n²) from the nested loop, with one extra step at the start that sorts everything in O(n log n). Memory use doesn’t change during the loop, so the extra space used while scanning stays flat. The only growth comes from whatever triplets get added to the final result list.

Solution 1: Hash Set and Unsorted Triplets — Copy and Paste

class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        Set<List<Integer>> result = new HashSet<>();
        int n = nums.length;

        for (int i = 0; i < n - 2; i++) {
            Set<Integer> seen = new HashSet<>();

            for (int j = i + 1; j < n; j++) {
                int complement = -nums[i] - nums[j];

                if (seen.contains(complement)) {
                    List<Integer> triplet = Arrays.asList(nums[i], nums[j], complement);
                    Collections.sort(triplet);
                    result.add(triplet);
                }

                seen.add(nums[j]);
            }
        }

        return new ArrayList<>(result);
    }
}

Solution 2: Sorted Scan with Two Pointers — Copy and Paste

class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        List<List<Integer>> result = new ArrayList<>();
        Arrays.sort(nums);

        for (int i = 0; i < nums.length - 2; i++) {
            if (i > 0 && nums[i] == nums[i - 1]) {
                continue;
            }

            int left = i + 1;
            int right = nums.length - 1;

            while (left < right) {
                int sum = nums[i] + nums[left] + nums[right];

                if (sum == 0) {
                    result.add(Arrays.asList(nums[i], nums[left], nums[right]));

                    while (left < right && nums[left] == nums[left + 1]) {
                        left++;
                    }

                    while (left < right && nums[right] == nums[right - 1]) {
                        right--;
                    }

                    left++;
                    right--;
                } else if (sum < 0) {
                    left++;
                } else {
                    right--;
                }
            }
        }

        return result;
    }
}