LeetCode #4: Median of Two Sorted Arrays — Solved in Java
Merge and Median and Binary Partition
This is the first hard problem on LeetCode, and it shows up a lot. It sounds easy at first. You’re given two sorted arrays and asked to find the median. But it gets tricky fast. You are not supposed to merge them if you care about performance. There’s a direct way that gives you the answer, and there’s a faster one that tends to come up in interviews. Both are shown below in Java, and we’ll go through each solution step by step.
LeetCode: Median of Two Sorted Arrays
Given two sorted arrays
nums1andnums2of sizemandnrespectively, return the median of the two sorted arrays.The overall run time complexity should be
O(log (m+n)).Example 1:
Input: nums1 = [1,3], nums2 = [2]
Output: 2.00000
Explanation: merged array = [1,2,3] and median is 2.
Example 2:
Input: nums1 = [1,2], nums2 = [3,4]
Output: 2.50000
Explanation: merged array = [1,2,3,4] and median is (2 + 3) / 2 = 2.5.
Constraints:
nums1.length == m
nums2.length == n
0 <= m <= 1000
0 <= n <= 1000
1 <= m + n <= 2000
-106 <= nums1[i], nums2[i] <= 106
Solution 1 — Simple Merge and Median (O(m + n))
Java Merge-Based Solution for Median
This version solves the problem by fully merging both sorted arrays into one list, then picking out the median. It’s not the fastest approach, but it’s easy to understand and works well when performance isn’t a big concern.
Let’s walk through it step by step:
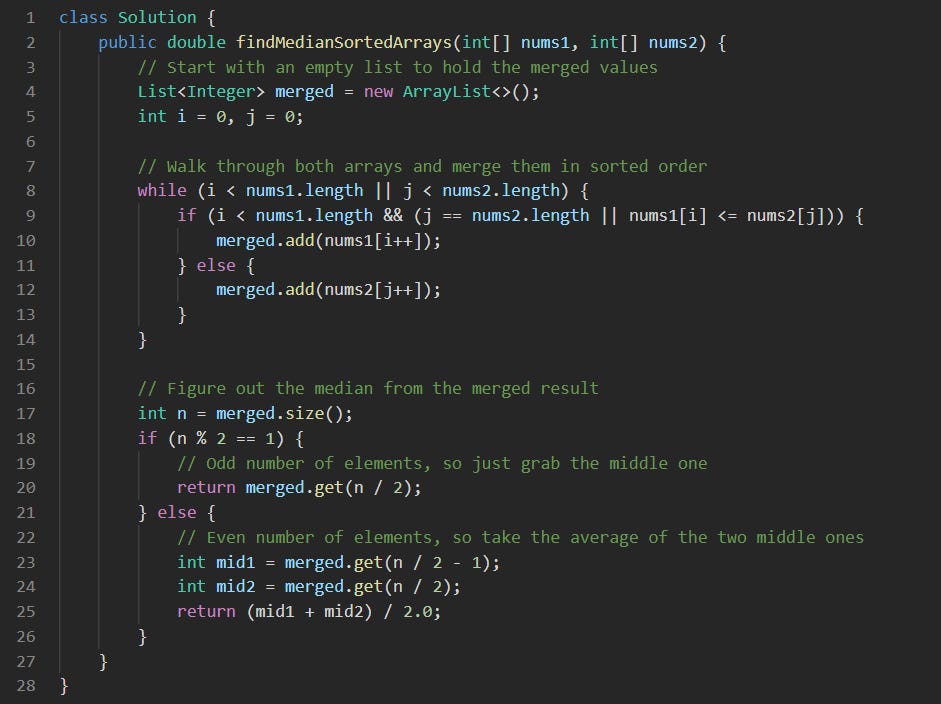
class Solution {This starts the class. No changes needed here.
public double findMedianSortedArrays(int[] nums1, int[] nums2) {We define the method. It takes two sorted arrays and returns their combined median as a double.
List<Integer> merged = new ArrayList<>();
int i = 0, j = 0;We create a new list to hold the merged values. Two pointers i and j will help track where we are in each array.
while (i < nums1.length || j < nums2.length) {This loop continues as long as we still have elements to pull from either array.
if (i < nums1.length && (j == nums2.length || nums1[i] <= nums2[j])) {
merged.add(nums1[i++]);
} else {
merged.add(nums2[j++]);
}Here we compare the current values from both arrays. If we haven’t finished nums1 and either we’ve already gone through nums2 or the value in nums1 is smaller, we take the value from nums1. Otherwise, we take from nums2. Each time, the value is added to the merged list, and the pointer is moved forward.
}The merging is complete. At this point, merged holds all elements from both arrays in sorted order.
int n = merged.size();We get the total number of elements in the merged list.
if (n % 2 == 1) {
return merged.get(n / 2);
}If the length is odd, the median is just the middle value. We return that directly.
else {
int mid1 = merged.get(n / 2 - 1);
int mid2 = merged.get(n / 2);
return (mid1 + mid2) / 2.0;
}If the length is even, we grab the two middle elements and return their average. The division is done with 2.0 to make sure the result stays a double.
}This closes the method.
This method walks through each array once, so the time complexity is O(m + n). Since it stores all the elements in a new list, the space complexity is also O(m + n). It’s a good starting point for solving the problem and works just fine when input sizes are small or when clarity is more important than raw speed.
Solution 2 — Interview-Ready Binary Partition (O(log(min(m, n)))
Java Optimized Solution for Median
This solution finds the median by doing a binary search instead of merging the arrays. It’s more efficient and better suited for large inputs or interview settings. It works by slicing both arrays in the right place so the left and right halves form a valid split around the median.
Let’s walk through it:
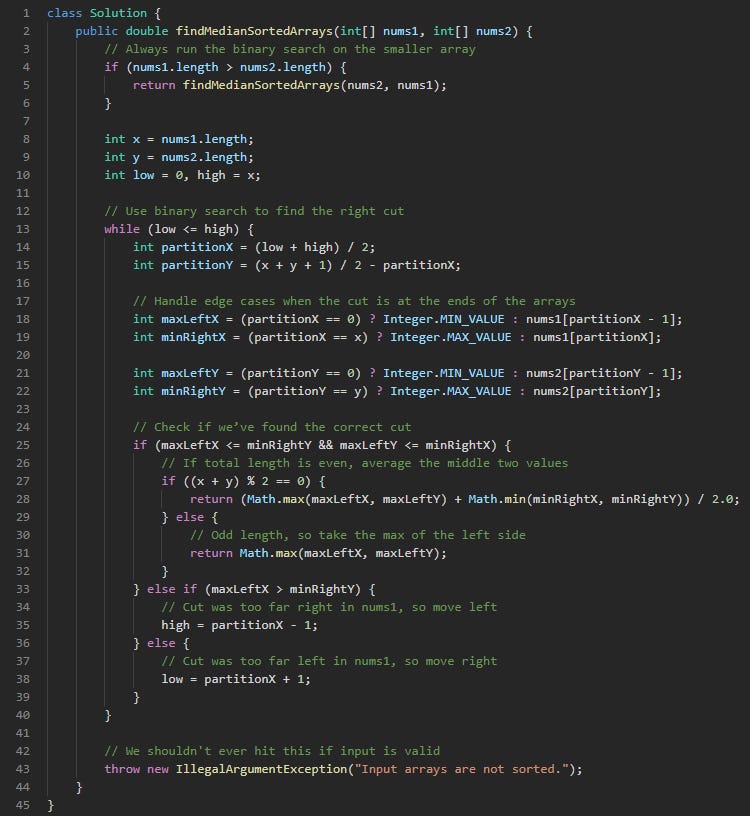
class Solution {This defines the class as expected by LeetCode.
public double findMedianSortedArrays(int[] nums1, int[] nums2) {This method takes in two sorted arrays and returns the median of their combined values.
if (nums1.length > nums2.length) {
return findMedianSortedArrays(nums2, nums1);
}To make the binary search simpler, we always search on the smaller array. If nums1 is longer, we flip the inputs.
int x = nums1.length;
int y = nums2.length;
int low = 0, high = x;We store the lengths of both arrays. The search will happen between low and high, which define the range for where the cut might go in nums1.
while (low <= high) {This loop performs the binary search. It keeps running until we find a valid partition.
int partitionX = (low + high) / 2;
int partitionY = (x + y + 1) / 2 - partitionX;We make a cut in nums1 at partitionX. Based on that, we calculate the matching cut in nums2 at partitionY so the total number of elements on the left side matches the right.
int maxLeftX = (partitionX == 0) ? Integer.MIN_VALUE : nums1[partitionX - 1];
int minRightX = (partitionX == x) ? Integer.MAX_VALUE : nums1[partitionX];These lines get the values just to the left and right of the cut in nums1. If the cut is at the start or end, we use placeholder values to avoid index errors. Integer.MIN_VALUE and Integer.MAX_VALUE help keep the logic valid without breaking comparisons.
int maxLeftY = (partitionY == 0) ? Integer.MIN_VALUE : nums2[partitionY - 1];
int minRightY = (partitionY == y) ? Integer.MAX_VALUE : nums2[partitionY];We do the same thing for nums2, grabbing values just to the left and right of its cut. Again, we guard the edges with extreme values if the partition lands at the start or end.
if (maxLeftX <= minRightY && maxLeftY <= minRightX) {This is the key check. If everything on the left is less than or equal to everything on the right, we’ve found the correct split.
if ((x + y) % 2 == 0) {
return (Math.max(maxLeftX, maxLeftY) + Math.min(minRightX, minRightY)) / 2.0;
} else {
return Math.max(maxLeftX, maxLeftY);
}If the total number of values is even, the median is the average of the two middle values. If it’s odd, it’s just the largest value on the left side.
} else if (maxLeftX > minRightY) {
high = partitionX - 1;
} else {
low = partitionX + 1;
}If the left side of nums1 is too large, we shift the binary search to the left. If it’s too small, we move to the right.
}This closes the binary search loop.
throw new IllegalArgumentException("Input arrays are not sorted.");
}This is a safeguard. The code should never reach this point if the input arrays are valid and sorted.
This version runs in O(log(min(m, n))) time because it only searches the smaller array. It doesn’t create new arrays or extra data structures, so space usage stays at O(1). The goal is to split both arrays so the left half and the right half fall on either side of the median. After that balance is found, the answer is right there in the edge values around the cut. It takes some getting used to, but it’s a strong solution that shows you understand binary search and problem structure at a deeper level.
Basic Merge and Median — Copy and Paste
class Solution {
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
List<Integer> merged = new ArrayList<>();
int i = 0, j = 0;
while (i < nums1.length || j < nums2.length) {
if (i < nums1.length && (j == nums2.length || nums1[i] <= nums2[j])) {
merged.add(nums1[i++]);
} else {
merged.add(nums2[j++]);
}
}
int n = merged.size();
if (n % 2 == 1) {
return merged.get(n / 2);
} else {
int mid1 = merged.get(n / 2 - 1);
int mid2 = merged.get(n / 2);
return (mid1 + mid2) / 2.0;
}
}
}Interview Version — Copy and Paste
class Solution {
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
if (nums1.length > nums2.length) {
return findMedianSortedArrays(nums2, nums1);
}
int x = nums1.length;
int y = nums2.length;
int low = 0, high = x;
while (low <= high) {
int partitionX = (low + high) / 2;
int partitionY = (x + y + 1) / 2 - partitionX;
int maxLeftX = (partitionX == 0) ? Integer.MIN_VALUE : nums1[partitionX - 1];
int minRightX = (partitionX == x) ? Integer.MAX_VALUE : nums1[partitionX];
int maxLeftY = (partitionY == 0) ? Integer.MIN_VALUE : nums2[partitionY - 1];
int minRightY = (partitionY == y) ? Integer.MAX_VALUE : nums2[partitionY];
if (maxLeftX <= minRightY && maxLeftY <= minRightX) {
if ((x + y) % 2 == 0) {
return (Math.max(maxLeftX, maxLeftY) + Math.min(minRightX, minRightY)) / 2.0;
} else {
return Math.max(maxLeftX, maxLeftY);
}
} else if (maxLeftX > minRightY) {
high = partitionX - 1;
} else {
low = partitionX + 1;
}
}
throw new IllegalArgumentException("Input arrays are not sorted.");
}
}