LeetCode #5: Longest Palindromic Substring — Solved in Java

Expand Around Center and DP Table

Image Source

This problem asks you to find the longest substring that reads the same forward and backward. You can't shuffle characters or skip around. It has to be one continuous stretch. One way to solve it is by checking every possible center. There's also a faster option that keeps track of what's already been checked to save time. You’ll see both versions written out in Java below, and we’ll go through each solution step by step.

LeetCode: Longest Palindromic Substring

Given a string s, return the longest palindromic substring in s.

Example 1:

• Input: s = "babad"

  Output: "bab"

  Explanation: "aba" is also a valid answer.

Example 2:

• Input: s = "cbbd"

  Output: "bb"

Constraints:

• 1 <= s.length <= 1000

• s consist of only digits and English letters.

Solution 1 — Expand Around Center (O(n²))

Java Center-Expansion Solution

This solution looks at every possible center of a palindrome and expands outward while the characters match. Every character, and every gap between characters, is treated as a center. This lets us catch both odd- and even-length palindromes.

Let’s go through it:

class Solution {

This defines the class. Nothing unusual here, it's just the structure LeetCode uses.

public String longestPalindrome(String s) {

We define a method that takes in a string and returns the longest palindromic substring inside it.

if (s == null || s.length() < 1) return "";

This checks for an empty input. If the string is null or has no characters, we return an empty result right away.

int start = 0, end = 0;

These two variables keep track of the start and end positions of the best palindrome we’ve found so far.

for (int i = 0; i < s.length(); i++) {

We loop through every index in the string. Each character can be a potential center of a palindrome.

int len1 = expandAroundCenter(s, i, i);
int len2 = expandAroundCenter(s, i, i + 1);

We check two possible centers for each position. len1 checks for an odd-length palindrome (centered at one character). len2 checks for an even-length one (centered between two characters).

int len = Math.max(len1, len2);

We pick the longer result of the two expansions.

if (len > end - start) {
start = i - (len - 1) / 2;
end = i + len / 2;
}

If this new palindrome is longer than the one we already had, we update the start and end pointers to reflect its range.

}

That finishes the loop through the string.

return s.substring(start, end + 1);
}

We return the substring from start to end. Adding 1 to end is needed because substring excludes the upper bound.

Now let’s look at the helper method:

private int expandAroundCenter(String s, int left, int right) {

This helper method takes two indexes, one for the left side of the center and one for the right.

while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {
left--;
right++;
}

While the characters at both ends match, and we’re still within the bounds of the string, we keep expanding outward.

return right - left - 1;
}

When we break out of the loop, we return the length of the last valid palindrome. We subtract 1 because the final mismatch expanded the window one step too far on both sides.

The time complexity is O(n²) in the worst case. That’s because each center might stretch across most of the string. Space usage is O(1) becasue we’re only using a few integer variables. This version is simple to understand and works well unless the input is very large.

Solution 2 — DP Table (O(n²) Time, O(n²) Space)

Java Dynamic Programming Solution

This version uses dynamic programming to track which substrings are palindromes. Instead of checking the same sections over and over, it stores the results in a table so we can build on what’s already been checked.

Let’s walk through it:

class Solution {

This defines the class. It's the standard structure used in LeetCode problems.

public String longestPalindrome(String s) {
if (s == null || s.length() < 1) return "";

We start by handling empty input. If the string is null or has no characters, we return an empty result right away.

int n = s.length();
boolean[][] dp = new boolean[n][n];
int start = 0, maxLen = 1;

We get the length of the string and create a 2D array named dp. Each dp[i][j] will be true if the substring from index i to j is a palindrome. start and maxLen help track the longest one we find.

for (int i = 0; i < n; i++) {
dp[i][i] = true;
}

Every single character is a palindrome by itself. This loop marks all those entries as true in the table.

for (int i = 0; i < n - 1; i++) {
if (s.charAt(i) == s.charAt(i + 1)) {
dp[i][i + 1] = true;
start = i;
maxLen = 2;
  }
}

Now we check for two-character palindromes. If two adjacent characters match, we mark them in the table and update start and maxLen if needed.

for (int len = 3; len <= n; len++) {
for (int i = 0; i <= n - len; i++) {
int j = i + len - 1;

We loop through all possible substring lengths starting from 3. For each length, we slide a window across the string. i is the start of the window and j is the end.

if (s.charAt(i) == s.charAt(j) && dp[i + 1][j - 1]) {
dp[i][j] = true;
start = i;
maxLen = len;
    }
  }
}

If the characters at the edges match, and the section in between is also a palindrome, then the whole substring is a palindrome. We mark it in the table and update our result if it's the longest one so far.

return s.substring(start, start + maxLen);
}

After filling in the table, we return the longest palindromic substring we found using the saved start and maxLen.

This one runs in O(n²) time because it checks all possible substrings. It also uses O(n²) space to store the dp table. It takes up more memory, but it avoids rechecking the same substrings repeatedly. That can save time when working with longer inputs. It’s a good approach when clarity and reuse are more important than keeping space usage minimal.

Expand Around Center — Copy and Paste

class Solution {
    public String longestPalindrome(String s) {
        if (s == null || s.length() < 1) return "";

        int start = 0, end = 0;

        for (int i = 0; i < s.length(); i++) {
            int len1 = expandAroundCenter(s, i, i);
            int len2 = expandAroundCenter(s, i, i + 1);
            int len = Math.max(len1, len2);

            if (len > end - start) {
                start = i - (len - 1) / 2;
                end = i + len / 2;
            }
        }

        return s.substring(start, end + 1);
    }

    private int expandAroundCenter(String s, int left, int right) {
        while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {
            left--;
            right++;
        }
        return right - left - 1;
    }
}

DP Table — Copy and Paste

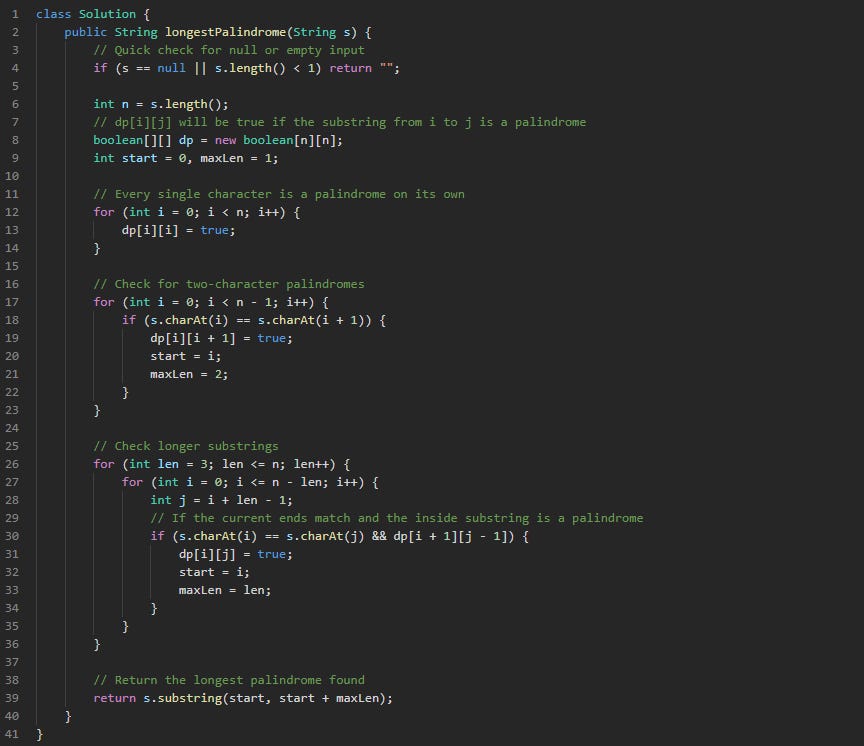
class Solution {
    public String longestPalindrome(String s) {
        if (s == null || s.length() < 1) return "";

        int n = s.length();
        boolean[][] dp = new boolean[n][n];
        int start = 0, maxLen = 1;

        for (int i = 0; i < n; i++) {
            dp[i][i] = true;
        }

        for (int i = 0; i < n - 1; i++) {
            if (s.charAt(i) == s.charAt(i + 1)) {
                dp[i][i + 1] = true;
                start = i;
                maxLen = 2;
            }
        }

        for (int len = 3; len <= n; len++) {
            for (int i = 0; i <= n - len; i++) {
                int j = i + len - 1;
                if (s.charAt(i) == s.charAt(j) && dp[i + 1][j - 1]) {
                    dp[i][j] = true;
                    start = i;
                    maxLen = len;
                }
            }
        }

        return s.substring(start, start + maxLen);
    }
}